
FIGURE 1
Dynamic programming determines the minimum not by means of derivatives as in the variational approach, but rather by a straightforward search technique. The minimization of the energy function can be viewed as a discrete multistage decision process. Thus we can apply the technique of dynamic programming. Starting from the initial point on the contour, we can treat the minimization problem as one that at each of a finite set of stages (i0, i1, ... in-1) corresponding to snaxel positions, a decision is chosen from a finite set of possibilities of positions within a small neighborhood to move that snaxel to give a minimum value.
A correspondence can be made between minimization of the total energy measure (considering only the first order term in the internal energy measure) and the problem of minimizing a function of the form
Eq. (*)
where each variable is allowed to only take on m possible values, generally corresponding to adjacent snaxel locations within the search neighborhood. One way to find the minimum of the above function is by exhaustive enumeration. A more efficient method is via discrete dynamic programming, with vi (the new snaxel location) corresponding to the state variable in the ith decision stage.
The dynamic programming solution involves generating the sequence of functions of one variable, {si} for i = [1,n-1] (the optimal value function), where for obtaining each si a minimization is performed over a single dimension, over vi. As an example, for a function having the form of (*) with n=5,
s1(v2) = min v1 {E1(v1,v2)}
s2(v3) = min v2 {s1(v2) + E2(v2,v3)}
.
s4(v5) = min v4 {s3(v4) + E4(v4,v5)}
min over v1...v5 of E = min v5 {s4(v5)}
For the general case, .
In view of the form of (*), let us first
consider only the first order term in
Eint, With k representing the
stage and vk being the state variable , the recurrence relation for
computing the optimal value function for contours is given by
sk(vk+1) = min vk {sk-1(vk) + Eext(vk) + |vk+1 - vk|^2
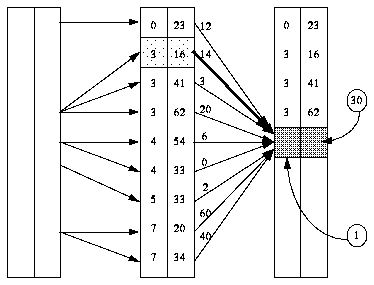
FIGURE 2
Figure 2 shows the basic idea in a case where there are nine possible states per stage (this corresponds to each entry in a 3x3 grid of neighbors centered at the current snaxel position). The cost associated with any given arc corresponds to the internal energies of the possible choices in decision sets.
In addition to the energy matrix corresponding to the optimal value function {sk}, a position matrix is also needed. Each entry of the position matrix at stage k stores the value of vk that minimizes Eq. (**). In order to find the contour of minimum energy using the backward method of solution for discrete dynamic programming problems, Emin(t) = min over vn {sn-1(vn)} is found. This is the total energy of the new optimal contour. Tracing back in the position matrix, the optimal contour is found. This procedure constitutes a single iteration. If there are n points and m directions at each point, each of the n iterations has complexity O(nm^2). For finding the optimal contour, the iterative process continues until Emin(t) does not change with time. Convergence is guaranteed since the configuration of points on the contour will not change unless the total energy of the contour is reduced by the new configuration.
An important feature of this algorithm is that one is able to enforce hard constraints on the solution. Consider for example the case of an inequality constraint where it is desired that no two adjacent points on the contour become closer that a distance d. In such a situation, when computing the energy matrix, the distance between points are also computed. If computing sk(vk+1) yields a point that violates the distance constraint for some value of vk, then that choice is eliminated and the next best minimum satisfying the constraint is chosen. In this case the value of the new minimizer of vk is stored in the position matrix. If no minimum exists which satisfies the constraint the algorithm halts. Another useful example of a hard constraint might be a binary edge image.