Asynchronous Iterative Methods

A parallel asynchronous iterative method for solving a system of equations is one in which processors do not synchronize at the end of each iteration. Instead, processors proceed iterating on the equations assigned to it with the latest data that is available from other processors. Running an iterative method in such an asynchronous fashion may reduce solution time when there is an imbalance of the effective load between the processors. Solution time may also be reduced when communication costs are high because computation continues while communication takes place.
We have developed asynchronous versions of multigrid and domain decomposition methods. Our work has also led to surprising findings, such as the fact that the asynchronous Jacobi method can converge when the corresponding synchronous method does not converge. This fact does not contradict theory, but arises from studying the practical behavior of asynchronous iterations.
Hierarchical Matrices

Kernel matrices in machine learning and scientific applications have hierarchical block low-rank structure that can be exploited so that storage and algorithms with these matrices are scalable. We have developed fast methods for computing and using the hierarchical matrix representation that are specialized for various application problems, including Gaussian processes, Brownian dynamics, and quantum chemistry.
Parallel Quantum Chemistry
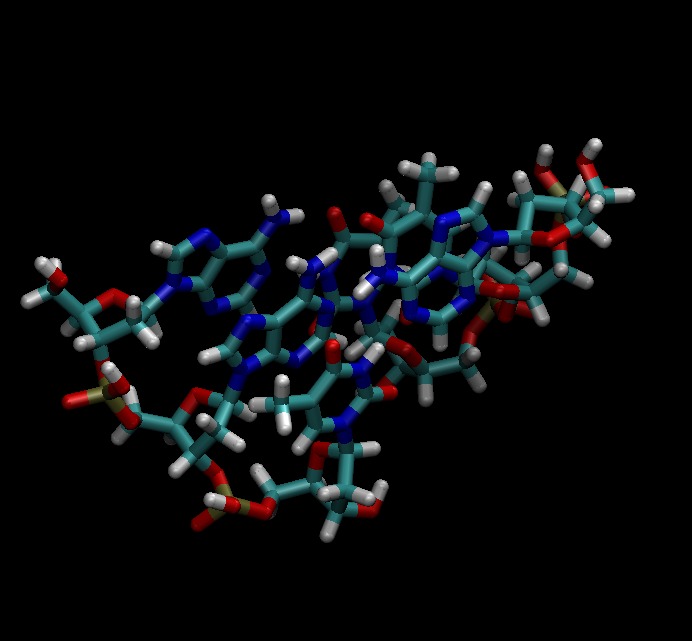
Our long-term goal for this project is to scale quantum chemistry calculations to millions of processor cores. Hartree-Fock or self-consistent field (SCF) calculations are typically compute-bound, due to computationally intensive electron repulsion integral (ERI) computations. However, the calculation is very irregular, and on large distributed memory supercomputers, unbalanced communication will easily ruin scalability. We have developed partitioning methods and distributed dynamic scheduling techniques to reduce and balance communication costs. This work won the Best Paper Award (Applications Track) at IPDPS 2014.
Brownian Dynamics with Hydrodynamic Interactions
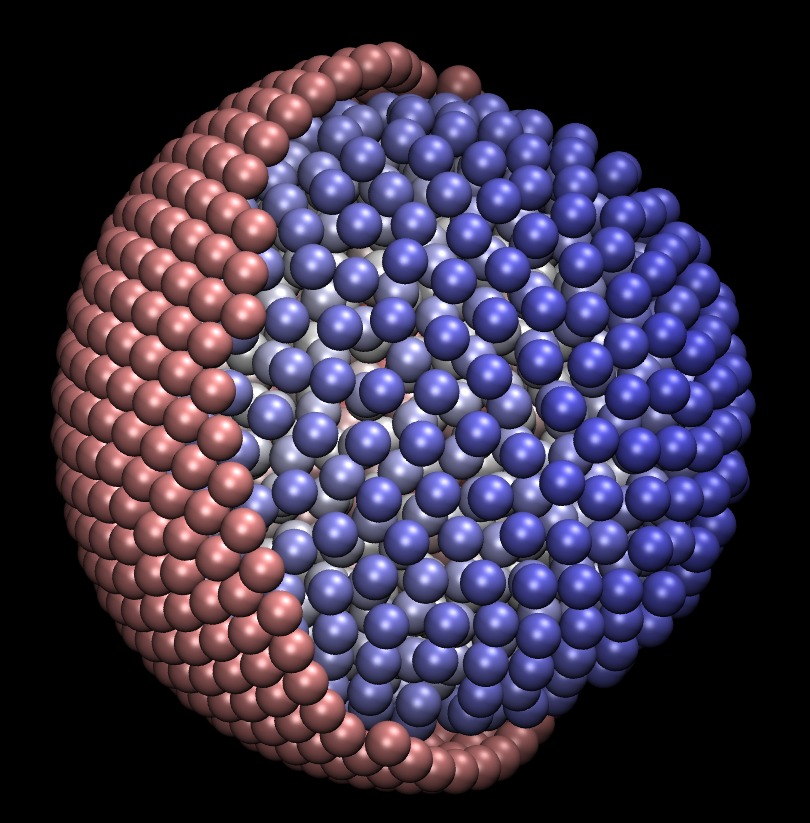
Particle simulations involving long-range forces (such as hydrodynamic, electrostatic, and gravitational) become challenging at large scales because every particle interacts with every other particle. Luckily, some fast algorithms exist. We are applying the FFT-based particle-mesh Ewald method to Brownian dynamics and Stokesian dynamics for non-dilute systems when hydrodynamic forces are dominant. One application is the modeling of diffusion processes inside biological cells (see figure to the left). These types of particle simulations are rich in problems for numerical linear algebra. For example, we were led to discover how to precondition Lanczos methods for computing Brownian forces, a technique that can also be applied to statistical simulation in other domains. Our implementations of PME can simulate hydrodynamic systems involving 500,000 particles, probably the largest ever performed on a single node.
Matrix Computations on Fine-Grained Computer Architectures
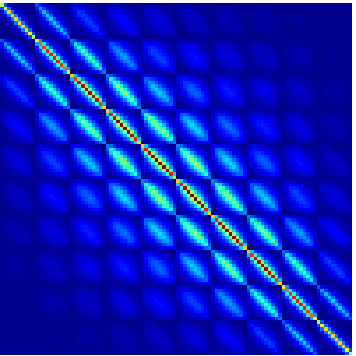
We are developing new algorithmic techniques to exploit the large number of cores and wide SIMD available on today's processors. Our software for the sparse matrix-vector product kernel, using a data structure we call ELLPACK Sparse Block (ESB), has been released by Intel as a prototype package.
Our work addresses the problem of the massive fine-grained concurrency required in scientific and engineering algorithms in order to run efficiently on current and future computer architectures. Some of the most effective algorithms are inherently sequential, but we break up this sequential bottleneck by applying approximations and iterations. We focus on certain matrix factorization problems arising in scientific and engineering simulation and data analysis, for example, incomplete factorization preconditioners and matrix completion problems.