|
|
 |
|
Multi-Agent Reinforcement Learning
Multi-agent reinforcement learning (MARL) poses the same learning problem as traditional reinforcement leaning (RL): How can an agent learn to maximize their rewards through interaction with their environment? Traditional RL has formalized this problem by modeling the environment as a Markov decision process (MDP) where the outcome of our agent's actions are fully explained by the state the world is in. MDPs work well for modeling simple dynamic systems but have a hard time modeling the near boundless complexity of the real world. A particularly interesting class of environments that MDPs model poorly can be understood, instead, by modeling them as a relatively simple process, but with complex dynamics attributed to the presence of other agents who are also attempting to maximize their rewards. MARL addresses the RL problem in these environments using stochastic (Markov) games (Littman 1994) as the formal model.
The field of game theory has long addressed the question of how to model and predict the behavior of multiple self interested agents acting in the same environment. Game theory is a mature discipline containing some of the best answers we have to how competing agents will act. MARL has taken much, as it should, from game theory. However, there are three fundamental problems preventing game theory from being directly applied to the MARL problem.
- Few algorithms that compute general-sum game theoretic solutions efficiently scale beyond toy problems.
- Game theory assumes agents are fully rational, meaning they have infinite intelligence and computational power, an assumption that clearly does not hold in the real world.
- Due in large part to the first two problems, game theory has a descriptive focus on properties of ideal behavior and mechanism design while on the other hand MARL primarily has a prescriptive focus on designing algorithms for optimal control in potentially unknown environments.
My thesis primarily attempts to address the first shortcoming and utilize game theory's strong theoretical foundation to solve the multi-agent reinforcement learning problem. We accomplish this by designing scalable algorithms to compute game theoretic solutions for stochastic games of complete and incomplete information. Under certain restricted circumstances these results can be directly applied, while without scalable algorithms game theoretic results are not practicable (even if the other two shortcomings are addressed). Once we have efficient algorithms the last two shortcomings can be overcome by modeling bounded rationality and the need for exploration as unknown variables in a known game of incomplete information.
Completed Work
My solution revolves around using \emph{achievable set functions} as the basis for computation and communication. This is a similar approach to related work in both operations research (Abreu 1988; Cronshaw 1997; Judd, Yeltekin, and
Conklin 2003; Horner et al. 2010) and MARL (Murray and Gordon 2007; Burkov and Chaib-draa 2010). However, none of these approaches has appealing error or computational guarantees able to generalize to stochastic games (SGs). An achievable set function is the multi-agent analogy to the single agent value-function. As a group of agents follow a joint-policy, each player receives rewards. The discounted sum of these rewards is that player's utility. The vector containing these utilities is known as the joint-utility, or value-vector. Thus, a joint-policy yields a joint-utility. If we examine all mixed joint-policies, discard those not in equilibrium, and compute all the joint-utilities of the remaining policies we will have a set of points in R^n (one dimension for each player's utility) -- the achievable set, depicting which joint-utilities are achievable (Figure 1).
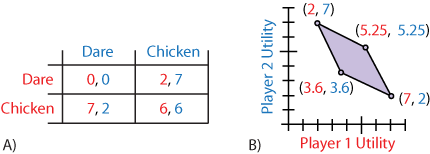 |
|
Figure 1: A) The game of chicken. B) The achievable set of correlated equilibria for chicken. For each joint-utility within the region there exists a correlated equilibrium yielding those rewards for each player.
|
In MacDermed & Isbell (2009) we show how to efficiently approximate with bounded error the achievable set in stochastic games. This is the first work to give such guarantees. Although theoretically the guarantees in this work promise the first polynomial efficiency and precision guarantees along a number of dimensions, practically the work requires solving sequences of multi-objective linear programs which in practice are quite slow and still limit the complexity of the stochastic games they can solve. In MacDermed et al. (2011) we show how to make this computation even more efficient by representing achievable sets as polytopes (intersections of half-spaces) instead of convex hulls. This results in solving a series of linear programs instead of multi-objective LPs and allows stochastic games with many more actions and a few more players to be tractably solved with greater precision.
The above work all assumes complete information (including knowing the other player's reward function). Although in some scenarios this is a reasonable assumption (for example in mechanism design), in most cases either the other agent's goals aren't exactly known or the other agent doesn't perfect act in accordance with their goals (bounded rationality). Both cases can be modeled as playing a game with incomplete information. Towards this end we have developed a new model: Markov games of incomplete information (MGII) (Mac Dermed, Isbell, and Weiss 2011). This model is distinct from and a subset of the existing model of partially observable stochastic games (POSG), in that MGIIs prevent the formation of nested beliefs and permit a bounded enumeration of private information (types) while POSGs do not.
While solving stochastic games of incomplete information are extremely difficult (POMDPs are a special case) we have shown how our solution to the complete information case can be extended to the incomplete case when belief states obey the Markov property and are chosen independently at random every state. This can model both uncertainty and noise over other players' preferences leading to more robust policies. We also argue that such uncertainty and noise can capture the bounded rationality of other players and diminish our results' sensitivity to the assumption of rationality.
Future Work
Although I have shown how to compute correlated equilibria in stochastic games efficiently with respect to the number of states and actions, I propose to improve scalability with respect to the number of players and unknown variables, both of which currently scale exponentially for all known methods. Also, while the achievable set method has been tested extensively on random Markov games and small games with known closed form solutions, I propose to apply our algorithms to a number of real world applications. Thus my dissertation will attempt to demonstrate that achievable set methods can efficiently compute useful game theoretic solutions to general multi-agent reinforcement learning problems.
I will address the problem of scalability by developing a new hybrid model that will merge action-graph games with stochastic games. Instead of playing a sequence of normal-form games (which are exponential in the number of players), agents will play a sequence of action-graph games. Action graph games compactly represent the interaction between many agents by taking advantage of symmetry and independencies in the structure of the game. Extending this compact representation to stochastic games is non-trivial as both asymmetries and dependences persist over time.
While complex, such a model will not only help with scaling the number of players but also the number of unknown variables in games of incomplete information. MGIIs can be solved by transforming them into completely observable games with many players, one for each type. These games however have a great deal of structure which can be captured by action-graph games and exploited to produce more efficient algorithms.
Finally I propose to demonstrate the practicality and usefulness of these approaches by applying them to real world problems. For the complete information case, we will solve a multi-agent package delivery domain and test our results against other learning algorithms. For the incomplete information case we plan to examine different reputation metrics and examine their theoretical effectiveness in simulated buyer-seller environment with limited communication.
References
Abreu, D. 1988. On the theory of infinitely repeated games
with discounting. Econometrica 56(2):383-96.
Burkov, A., and Chaib-draa, B. 2010. An approximate
subgame-perfect equilibrium computation technique for repeated
games. In Twenty Fourth AAAI Conference on Artificial
Intelligence (AAAI '10).
Cronshaw, M. B. 1997. Algorithms for finding repeated
game equilibria. Computational Economics 10(2):139-68.
Horner, J.; Sugaya, T.; Takahashi, S.; and Vieille, N. 2010.
Recursivemethods in discounted stochastic games: an algorithm
for delta -> 1 and a folk theorem. Econometrica.
Judd, K. L.; Yeltekin, S.; and Conklin, J. 2003. Computing
supergame equilibria. Econometrica 71(4):1239-1254.
Littman, M. L. 1994. Markov games as a framework for
multi-agent reinforcement learning. In Proc. 11th International
Conf. on Machine Learning (ICML), 157-163. Morgan
Kaufmann.
Mac Dermed, L., and Isbell, C. L. 2009. Solving stochastic
games. In Advances in Neural Information Processing
Systems 22. 1186-1194.
Mac Dermed, L.; Narayan, K. S.; Isbell, C. L.; andWeiss, L.
2011. Quick polytope approximation of all correlated equilibria
in stochastic games. In Twenty Fifth AAAI Conference
on Artificial Intelligence (AAAI '11).
Mac Dermed, L.; Isbell, C. L.; and Weiss, L. 2011. Markov
games of incomplete information for multi-agent reinforcement
learning.
Murray, C., and Gordon, G. J. 2007. Multi-robot negotiation:
Approximating the set of subgame perfect equilibria in
general-sum stochastic games. In Advances in Neural Information
Processing Systems 19. 1001-1008.
|
|
|
|
 |
|