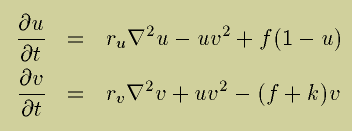Project 3: Reaction-Diffusion
CS 7492, Spring 2021
Due: TBD
Objective
This assignment will give you experience in solving partial
differential equations (PDE's) using finite differencing techniques.
In particular, you will simulate a reaction-diffusion system
known as Gray-Scott. This system creates patterns of spots,
stripes or spiral waves, depending on the parameter settings. One
aspect of this assignment is learning about how to implement
a diffusion operator.
Another aspect of this project is creating an image that gives a
map of the parameter space of the simulation system.
Finite Difference PDE Simulation
You will write a PDE simulator using finite differencing on a 2D grid.
The specific system you will simulate is known as the Gray-Scott
reaction-diffusion system. The equations that govern this system
are:
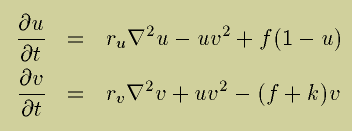
Central to your simulator will be a 2D grid, each cell of which
contains the concentrations of two chemicals, u and v. At each
timestep, the chemical concentrations at each cell will change
according to the above reaction-diffusion equations. As we
discussed in class, you should use operator splitting to separate the
reaction step from the diffusion step. This will allow you to
implement the forward Euler diffusion operator in a separate function.
Here are some characteristics of your simulator:
- Create a 2D grid that is at least 100 by 100 cells in size. (You may want to debug at lower resolution, however.)
- Draw each cell as a uniformly colored square that is at least 4
by 4 pixels in size. The gray-scale color should reflect chemical
concentration.
- You are free to choose what kinds of boundaries you use
(toroidal, zero derivative, fixed value, etc.).
Your simulator should act on this group of keyboard commands:
- i,I - Initialize the system with a fixed rectangular region that has specific u and v concentrations (more on this below).
- space bar - Start or stop the simulation (toggle between
these).
- u,U - At each timestep, draw values for u for each cell (default).
- v,V - At each timestep, draw values for v.
- d,D - Toggle between performing diffusion alone or reaction-diffusion (reaction-diffusion is default).
- p,P - Toggle between constant parameters for each cell and spatially-varying parameters f and k (more on this below).
- 1 - Set parameters for spots (k = 0.0625, f = 0.035)
- 2 - Set parameters for stripes (k = 0.06, f = 0.035)
- 3 - Set parameters for spiral waves (k = 0.0475, f = 0.0118)
- 4 - Parameter settings of your choice, but should create
some kind of pattern. Use your spatially-varying parameters image
to find good values for k and f.
- (mouse click) - Print values for u and v at cell. If in spatially-varying parameter mode, also print values for k and f at the cell.
Initialization: The
Gray-Scott reaction-diffusion system is quite sensitive to its initial
conditions. If you begin with entirely random cell values, it is
not likely to generate interesting patterns. To initialize your
grid of cells, first set each cell to have values u = 1, v = 0.
Then, within a 10 by 10 block of pixels, set the cell values to
be u = 0.5, v = 0.25. If you like, you can add small random
values to u and v within the cells of the block. You should feel free
to create more than one such block if you want to break up the symmetry
of the patterns that will form. Initially, your simulator should
begin in this initial state, and this is also the state that your
simulator should re-initialize to when you type the command "i".
Diffusion values: Fix the diffusion rate constants for u and v to ru = 0.082 and rv = 0.041.
Drawing the grid: At any given
time, your simulator should be displaying the values of either chemical
u or v. Each cell should have some gray-scale intensity based on
the chemical concentration. In order for you to see the full
range of values, find the minimum and maximum values for concentration
at the current timestep. Then scale the intensity so that the
lowest value is displayed as black and the highest value is white.
Since drawing the grid takes time, you may wish to modify your
simulator to display the grid just once every 10 timesteps.
Spatially-varying parameters:
In order to see the range of patterns that the Gray-Scott system,
the keyboard command "p" should cause your simulator to vary the
parameters k and f across different portions of the grid. The
parameter k should vary across the x direction (horizontally), and
should take on values between 0.03 and 0.07. That is, cells at
the left edge will have k = 0.03, cells at the right edge will have k =
0.07, and in-between cells will linearly vary in k between these two
extremes. The parameter f should vary in the vertical (y)
direction from f = 0.0 at the bottom to f = 0.08 at the top. When
you switch to this spatially-varying mode, you will find that small
grids do not show off these variations well. Change to a higher
resolution grid and let your simulator run in this mode for a fairly
long time in order to get a good picture of the parameter space.
When you have a good picture of the parameter space, pause your
simulator and take a snapshot of the current state of the simulator.
You will turn this in along with your source code. A
typical parameter space picture will look like this:

Diffusion solver: You
will write one diffusion solver, namely forward Euler diffusion.
For this diffusion solver, experiment with different values for
the timestep variable dt. Find the highest value for dt that
results in stable simulations.
As usual, we will use "Processing" to carry out this assignment:
http://www.processing.org/
For any large project such as this, I recommend backing up your
work often. You don't want to put in a ton of work and then accidentally
delete all of it. I suggest making a new copy of your entire work
folder every hour or so, and giving each new copy a higher number. Don't
worry about file sizes -- source files are tiny. I also recommend
copying all of your backups to a different computer once each day
for extra safety.
Suggested Approach
As usual, you can follow my suggestions or not, depending on your
level of confidence about this project.
Begin by creating a 2D floating point array for each of the u and v
cell values. Write a routine that will accept a 2D floating point
array and display it as an image of gray-scale intensity values.
You can debug this after you write the initialization routine
that makes a 10 by 10 block of special values (see Initialization above). You should be able to display a black square on a white background from the initialized values.
Once you can display your 2D cell values, it is time to start working
on forward Euler diffusion. Write a separate routine that accepts
a 2D floating point array as input, performs one time-step of
diffusion, and writes the result into the 2D array. This routine
should also have dt and the diffusion constant D as a parameters.
You will need a temporary 2D array in order to save intermediate values
for your diffusion calculation. Once you have calculated the new
values at each cell, copy these back into the 2D array that was passed
to the routine as input. Verify the operation of this routine by
calling it repeatedly for a non-constant array of values (e.g. the
initialized values for u), and drawing the new values on the screen.
It should blur out the initial dark square. If you have
trouble with this routine, print out the values for u for ONE cell and
its four neighbors, both before and after doing the diffusion step.
Do this for a cell at a dark/light boundary, and calculate by
hand what values you should expect to be printed. They key to
debugging PDE solvers is to only print out values for one or a few
cells, and to make sure that you have set up the values at that
location so that you can calculate by hand what the answer should be.
Often this means putting in special debugging code that you will
remove later. If your diffusion seems to work, experiment with
how large you can make dt before the routine becomes unstable.
Once you have forward Euler diffusion done, you are ready to move to
reaction-diffusion. Write a routine that accepts both the u and v
arrays and dt as parameters, and that modifies the u and v values
according to the reaction terms listed above. Remember that you
don't entirely replace u and v with the results of the reaction, but
instead you will change them slightly according to the magnitude of the
timestep parameter dt. Once you have this reaction operator, then
you are almost finished. Each step through your simulator loop,
perform diffusion on u with the diffusion parameter ku, perform
diffusion on v with kv, and then call the reaction operator. If
you initialize the cells as described above, then you should be able to
set k = 0.0625 and f = 0.035 and get a pattern of spots.
After you have one set of parameters working, make sure the other
parameters also behave correctly (stripes and spiral waves). You
should be able to switch between parameters during simulation by
pressing the 1, 2 or 3 keys. Once these work, it is time to add
spatially-varying parameters k and f. For this, you will modify
your reaction operator to act differently according to whether a global
flag is set. For spatially-varying parameters, use the cell
positions (x and y) to determine the values of k and f. Linearly
interpolate in each of these directions between the minimum and maximum
values given above. You will have to run the simulator at a
higher resolution than normal to get a really good picture of parameter
space.
Turning In Your Assignment and Spatially-Varying Parameter Image
Turn in your Processing code for this project on T-square.
In addition to your code, you should also include the image that shows the
effect of spatially varying the parameters (described above).
Authorship Rules
The code that you turn in must be entirely your own. You are allowed to
talk to other members of the class and to the teacher about general
implementation issues. It is also fine to seek the help of others for
general programming questions about Processing. You may not, however,
use
code that anyone other than yourself has written.
Code that is explicitly
not allowed includes code taken from the Web, from books, from previous
assignments or from any source other than yourself. You should not show
your code to other students. Feel free to seek the help of the teacher
for suggestions about debugging your code.