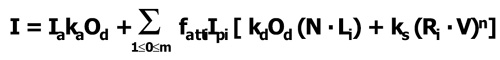Sample Questions

These questions are provided as examples of the kinds of questions you will be asked on the tests; at least half the questions on the tests will be taken from this set of questions. More questions will be added to this list over time.

These questions are not meant to provide complete coverage of the material covered. You are expected to know everything discussed in class, and the content of the book chapters listed on the syllabus.

3D Graphics Hardware

1. Pixels on LCD displays and CRT displays have a fundamentally different shape and appearance. (a) Describe the shape of an individual pixel on a CRT, and describe the physical construction of the CRT that creates this shape. (b) Explain why a white pixel contained in the interior of a large white area is brighter than a white pixel displayed in the middle of a large black area.
2. (a) A color look-up table is used to allow a large variety of colors to be displayed on a shallow frame buffer. Explain how. (b) Imagine you have an 4-bit deep framebuffer and you wanted to simulate having a more shallow frame buffer with a 1-bit overlay buffer. (An overlay buffer is a separate framebuffer whose contents are overlaid on the regular framebuffer. One specific "transparent" color in the overlay designates when the corresponding pixel from the framebuffer is displayed). How would you use a lookup table to create the 1-bit overlay where a 1 in an overlay pixel is "red" and a 0 is "transparent"? Draw the LUT and label the contents where appropriate. (c) How many different colors would you be able to have in your simulated shallow framebuffer?
3. Define the following terms:
   a) Resolution
   b) Addressability
   c) Color Lookup Table
   d) Pseudo Color
   e) Shadow Mask

Overview of 3D Graphics

1. What are the important differences between global and local illumination models? Why can local models be more easily implemented in hardware than the global models?
2. Ray tracing can create very realistic looking scenes. However, it is limited in the physical phenomena it can simulate. Describe the major problem with ray tracing (including describing why ray tracing cannot easily solve this problem) that the radiosity algorithm was designed to solve.

Modelling Overview (Polygonal, CSG, Volume, Implicit)

1. A typical data-structure for an object represented as a collection of polygonal faces stores an array of vertices, and represents the faces of each object by refering to the vertex list. Why do we start the vertex list in a separate array, rather than explicitely in the definition of each face? Give at least 2 reasons.
2. (a) Define each of these methods of modelling objects: CSG, Implicit functions, volumetric. (b) For each, describe a domain where the representation is more appropriate than a polygonal representation.

Modelling (Curves and Surfaces)

1. What is the degree of a polynomial necessary to fit n points? How many points of inflection does a curve defined by this polynomial have? Why do we usually use polynomials of degree 3 to represent curves?
2. Aside from piecewise polynomials, what are four techniques for representing objects in computer graphics? What are the advantages of using piecewise polynomials to represent objects with curved lines and surfaces over these other representations?
3. Compare Hermite, Bezier and B-spline representation of curves. Mention which curve characteristics are represented by the control points, the continuity of these representations, and the advantages and disadvantages of each representation.
4. What do we mean by the terms "non-uniform" and "rational" when discussing curve representations? What is the knot vector for a non-uniform B-spline that defines a B-spline that is equivalent to a Bezier curve?
5. Define the following terms: basis function, geometry matrix, control point, convex hull.

Basic 3D Math, Transformations, Vectors

1. Using the dot product, explain how one would determine if a face is front-facing (facing the view point) or back facing. Show the mathematical formulation you would use, and identify the coordinate system you are doing your computation in.
2. Why do we use homogeneous coordinates in computer graphics?
3. Are rotations commutative? What about translations? Give examples.
4. You are given a collection of models that were created using a modeling tool that defines the coordinate system with the XY plane parallel to the ground and Z as the height.OpenGL uses XY parallel to the screen (X rows, Y colunms) and -Z pointing towrds the monitor. How to convert the models from one coordinate system to the other?
5. (a) How do you compute a dot product? Why is it useful? (b) How do you computer a cross product? Why is it useful? What is a good way of visualizing a cross product? (c) What geometric entity is defined by the equation Ax + By + Cz + D = 0?
6. Let P, Q, and R be three points that lie in plane M. Give an equation for M's normal vector N, in terms of P, Q, and R.
7. Show the transformation matrix that would be used to perform each of the following transformations:
   1. Translate 4 units in the +x direction, 2 in -y, and 3 in +z.
   2. Scale by 3 in all dimensions.
   3. Rotate 90 degrees around the z-axis.
8. We create a transformation matrix by issuing the following OpenGL transformation commands:
   glLoadIdentity();
   glTranslate(0.0, 1.0, 0.0);
   glRotate(90.0, 1.0, 0.0, 0.0); /* rotate by 90 degrees about the x-axis */
   Then, we transform the point (0.0, 0.0, 1.0) by the matrix. What is the resulting point?
9. (a) How would you rotate an object, centered at position (3,2,-1), by D degrees around its own Y axis. Specify the components of the composite transformation matrix. (b) What are the steps for rotating an object by B degrees around an arbitrary axis, using the basic transforms discussed in class? Sketch diagrams to support your description, if necessary.
10. Assume you are using a sphere of radius 2 as the model of a woman’s head (assume the “nose” lies along the positive z axis and the “ears” are along the x-axis). You would like to rotate the head so that the model can “nod yes”. What point would be reasonable for the head to rotate about, in the local coordinate system. Assuming a right-handed coordinate system, what sequence transformations would you apply to nod the head 30 degrees forward?

Coordinate Systems and Viewing

1. Why does OpenGL uses 2 matrix 'stacks' to store the transformations? Give an example where using this separation is advantegeous?
2. Explain the sequence of coordinate systems in the standard 3D viewing process used in computer graphics. Mention the operations and transformations performed in each space.
3. What is back-face culling? What is it useful for? How to compute back faces?
4. Assume we wish to perform a simple perpective projection. Let d be the distance from the view plane to the center of projection. What is the matrix that projects a point p=(x, y, z) onto a point on the view plane p'=(x', y')?
5. The canonical view volume maps the visible part of the world to have Z values in the range [0..1]. Typical computer graphics hardware uses a fixed number of bits to represent Z. Discuss the consequences of this.
6. What are the parameters used in the PHIGS viewing model? Distinguish what is specified in World Reference Coordinate (WRC) and what is in View Reference Coordinate (VRC). We used a slightly different formulation in class than is in the book. Explain which parameter we ignored in class, and what the effect of ignoring that parameter is.
7. You are given a viewpoint for a virtual camera in 3D space (P1), a point the camera is looking at (P2) and a 3rd point (the “up” point, P3) that specifies which direction is up.
   1. What is the sequence of transformations that must be composed to create the simple perspective viewing transformation matrix? Write out the sequence of transformations symbolically (don’t write out the matrices, but rather define each matrix using words). For example, one of the transformations is “Mper”, the perspective matrix. Make sure you clearly define what each matrix does.
   2. How would you derive the required rotation matrix in your sequence from the inputs P1, P2, and P3?
   3. As discussed in class and the text, it is useful to think of last of the steps required to transform the visible viewing volume into the canonical parallel volume (referred to as Mper above) as two separate steps (Mper1 and Mper2). Write out these two matrices, labelling any constants you use on the supplied diagram.
      

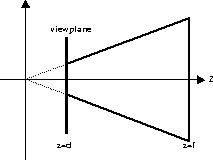
      Mper = Mper2 * Mper1
      Mper1 =

       

      Mper2 =

       

Clipping and Picking

1. What is the OpenGL window and the viewport? What are they used for?
   On which coordinate systems are they specified?
2. What is clipping? What is culling? Why is culling important and useful, even though clipping is typically implemented in hardware and culling in software? How can culling be implemented relatively efficiently? What are the pros and cons of the approach you describe?
3. Assume you have an application window that is 500x500 pixels in size. Within that, you set the viewport for OpenGL to have an origin of (10,20), a width of 100 and a height of 80. The user clicks at 50, 50. What is the position in the canonical view volume of the pixel under the user's mouse pointer? (show your work!)
4. Assume you wanted to clip lines to a view volume that is the diamond (square rotated by 45 degrees) with corners at (0,1) (1,0), (-1,0) and (0, -1). What are the formula you would use to compute the 4 1 bit outcodes? Draw the region, showing the region corresponding to each of the valid outcodes. For the edge between points (-1,0) and (0,1), how would you compute the intersection point of a line with that edge (show the math!)?
5. What is the transformation matrix created by gluPickMatrix(40, 30, 4, 4, {0, 0, 100, 100})? You may specify your matrix as the composition of more basic matrices; you do not have to multiply the matrices together to get the final matrix.(Recall that the parameters are the x,y position of the mouse, the width and height of the picking region, and the viewport OpenGL is using for display).

Lighting and Shading

1. Consider a room like our classroom, where the lights are recessed slightly into the ceiling. There is no way to directly trace a ray from any light source to a ceiling tile, and yet we can see them. Why is it that we can see them? How do we typically reproduce this effect in computer graphics?
2. The basic illumination equation discussed in class is shown here:
   1. Define each of the following terms:
      1. Ia
      2. ks
      3. Ri
      4. m
      5. n

   For questions b) and c), assume you are given a set of N vertices and a set of M polygons, each of which is defined as a sequence of the vertices. The polygons form a connected polygonal surface. Give short, concise answers (not algorithms) to each of these questions.

   2. If we want to use Flat Shading to color the polygons, how do we compute the color of each polygon?
   3. If we want to use Gouraud shading to smoothly shade the polygonal surface created by the polygons, how do we compute the color of each pixel?
   4. Why do we not typically use the specular term in the illumination equation when doing Flat and Gouraud shading?
3. What are three problems created by interpolating shading? Explain the problem, give examples of it in practice, and propose solutions.
4. The color for pixels has RGB components in the range [0..1]. We mentioned in class that light intensities can fall outside the range of [0,1]
   1. In OpenGL, you often need to specify a light intensity of > 1. Why is this necessary and how do we still end up with valid pixel colors?
   2. What would be the effect of having a light with intensity less than zero?

Rasterization, Hidden Surface Removal, Accumulation Buffers

1. 2D Line Rendering
   Here is the basic 2D line drawing algorithm, which draws a line from (0,0) to (a,b) in the first octant (line slopes between 0 and 1.

        x := 0;
        y := 0;
        d := b - a/2;
        for i := 0 to a do 
           Plot(x,y);
           if d >= 0 then
              x := x + 1;
              y := y + 1;
              d := d + b - a;
           else
              x := x + 1;
              d := d + b;
           end;
        end;

   In the questions below, you can refer to program lines using the line numbers. When you change a line, just show the new code with the appropriate line number. To insert a line, use decimal line numbers (e.g., 11.1 goes between 11 and 12).

   1. Modify the program to remove the division by 2 on line 3.
   2. Modify the program to allow the starting point to be any point, not just (0,0). The program still only needs to support lines whose slopes are in the range (0..1).
   3. Modify the program to draw lines in the 6th octant, assuming the start point is (0,0) and the end point is (a,b).
2. What is the computational complexity of the basic DDA line drawing algorithm? What about Bresenham's line drawing algorithm? What makes Bresenham's algorithm more efficient than the basic DDA?
3. What is the computational complexity of the scan-line polygon rasterization algorithm? Name two potential problems that must be addressed to properly rasterize a polygon, and describe how these problems are handled by the scan-line algorithm discussed in class.
4. Z-buffering and Backface Removal are two techniques that can be supported efficiently in 3D graphics hardware, because they can operate on the objects after they have been transformed to the canonical viewing volumes (right before they are rendered). Given a triangle whose points are P1, P2, and P3 in screen coordinates (i.e. after all transformations have been applied, right before rendering), how do we perform backface removal?
5. What is the Painter's algorithm? Give an example where the straightforward implmentation of this algorithm does not work. How would you deal with this example?
6. What is the advantage of using halftoning instead of simple grayscale?
7. BSP Trees
   1. What factors affect the decision of whether to use a BSP tree in rendering?
   2. Name an application for which a BSP would be a good idea, and one for which it would be a bad one.
   3. What is the average number of computations required to construct a BSP tree, in terms of the number of polygons N?
   4. What is the average number of computations required to render a scene properly using a BSP tree, assuming the tree is alreaedy constructed, but there are N polygons in the scene that were not included in the tree?
8. Filling Polygons
   1. In class, we discussed filling polygons with a pattern. Assuming the pattern is defined as a 0-based,
      m x n array, state a function to compute which element of the pattern is used for pixel (x,y) in the polygon. Use this algorithm to fill the pixels of the polygon shown below with the pattern shown.
   2. Explain how this function for filling a polygon with a pattern exhibits unsatisfactory side effects when a patterned polygon is translated around the screen. How would you change the function in a) so that this problem is avoided under translation? Under what conditions does your new function exhibit similar problems?

Mapping

1. What is texture mapping? How does it speed up 3D graphics? What is mipmapping, and how does it speed up texture mapping?
2. What is bump mapping? Why was bump mapping impractical in fast, interactive graphics until recently? What feature of modern graphics hardware has made bump mapping practical?
3. What is environment mapping? Name two techniques for creating environment maps, one that is appropriate for synthetic maps, and one for real scenes? How would you create environment maps for each of these two techniques?

Local Reflection Models

1. The BRDF
   1. What does acronym BRDF stand for?
   2. What does the term mean? In other words, what kinds of surfaces and/or illumination models does this function attempt to model? (you may contrast the BRDF with other models if that helps you define the meaning of this term)
   3. What are the four parameters to a BRDF?
2. What is the difference between Anisotropic and Isotropic surfaces?
3. How does the BRDF rendering equation handle the specular illumination created when the light and viewer are almost parallel with the object surface (i.e., the "road glare" problem)?
4. Motion capture is generally accomplished by using a set of cameras that shoot light into a room. Markers placed on some object reflect the light back at the cameras; this is how the cameras can detect the locations of the markers. The markers of made of an anisotropic substance that reflects light back in the direction it came from. What would be a good approximation of a mocap marker's BRDF?

Shadows

1. How do stencil buffers work? What are two things they are useful for (aside from shadow algorithms)?
2. Explain, in a few sentences each, the 4commom "fast" shadow techniques discussed in class.
3. What are the limitations of each of the 4 shadow techniques?

Retained Mode Graphics

1. What are two advantages of retained mode graphics (like Inventor or Java3D) over immediate mode graphics (like OpenGL)?
2. Describe two efficiency optimizations that can be performed by a retained mode graphics package that would be hard (or at least very tedious) for a programmer to implement themselves when using a package like OpenGL? Why would each be hard to implement?
3. When implementing a retained mode graphics library, you may need to traverse the scene graph more than once to update the screen. Describe what is done during each of three of these traversals, and state the order that the three you describe would be done in.
4. What are the advantages and disadvantages of using attribute inheritance in a hierarchical scene representation?
5. How do OpenGL display lists optimize rendering time? Why we need Scene graphs in addition to Display Lists?

Animation

1. What are Euler angles? What are two problems with using Euler angles to specify the orientation of an object when we want to interpolate between these orientations during an animation? What are quaternions, and why do they not exhibit the same interpolation problem as Euler angles?
2. What are articulated structures? Describe the two approaches (forward- and inverse-kinematics) to animating articulated structures.
3. What are three principles from traditional animation that have been used effectively in computer animation? Give pratical examples of each.

Volume Rendering

1. In volume rendering there are image-order methods (such as ray-casting) and object-order methods (such as splatting). In principle these methods should give nominally the same results for the same levels of accuracy, but in practice they do not.
   1. Discuss the advantages and disadvantages of each class of methods and the artifacts that can result from each.
   2. Which artifacts can be removed, and how?
   3. What is the relative computational complexity of the two classes of methods, taking into account sub-sampling for compositing.

Aliasing

1. Aliasing is a problem that we constantly encounter in computer graphics.
   1. What is aliasing and where does it come from?
   2. Give examples of both spatial and temporal aliasing that can occur in computer graphics, and discuss how each can be overcome.
2. Which of the following three rendering artifacts are a result of aliasing? For each of them, say *why* each is or is not aliasing.
   1. You are looking at a rendering of a building interior for which radiosity was used to calculate the shading on the surfaces. You can spot portions of the scene at which there are shading discontinuities where the underlying radiosity patches meet.
   2. You have just implemented the standard Bresenham line drawing algorithm, and your lines have a stair-step appearance.
   3. You are rendering an image with textures using OpenGL on typical 3D hardware. Your viewpoint is so close to one textured object that the individual pixels of the texture are clearly visible as big square blocks.
3. For the following two graphics applications, describe the consequences of NOT performing anti-aliasing to create the rendered images.
   1. A flight simulator for training fighter pilots.
   2. Computer graphics special effects that are to be mixed with live action in a movie.

Image-based Rendering

1. What is the basic motivation behind Image Based Rendering techniques?
2. What are impostors? How do they work? Explain when a new impostor needs to be computed.
3. Explain two approaches to add depth information to 2D IBR techniques. What are the pros and cons of each approach?
4. A simple light field uses a 5D function to define luminance. What are the 5 dimensions? The Lumigraph technique uses just 4D instead of 5D. What are the 4 dimensions, and why does this simplification work?

Global Illumination: Ray Tracing and Radiosity

1. What are the two traditional methods used for Global Illumination? How does each work? What simplifications to "perfect" global illumination do each make to be computationally tractable? What kind of scenes are best rendered with each of them?

Ray Tracing

1. What is two pass ray tracing? What illumination effects is it useful for? How does it work?
2. A significant problem with ray tracing (backwards ray tracing, or Whitted ray tracing, in particular) is that it samples only those properties of the surfaces that can be simulated by a single ray passing through a pixel and interacting with the scene. Much research has gone on, attempting to understand how to improve on the basic model while still being computationally tractable.
   Compare adaptive super sampling, path tracing and distributed ray tracing, summarizing how each works, how each tries to remove aliasing effects from the Whitted model (i.e., what additional effect do they allow, or problems can they solve), how they remain computationally tractable, and their relative cost.
3. When intersecting a ray with a sphere, we solve a set of equations to obtain values for the parameter t. What does
   t represent? When we solve the intersection equation, we could obtain zero, one or two values for t. What is the
   geometrical explanation for each of these three cases?
4. What are 3 techniques that we can use to increase the efficiency of the basic ray tracer implemented in
   assignment 5? (Do not simply name each technique, but also describe briefly how it works)
5. The basic illumination equation discussed in class is shown here:
   Rewrite this equation to include terms implementing reflection, transparency and shadows.
   

Color

1. Visible light corresponds to the visible wavelengths of light. A single color is most accurately represented as an continuous function of the visible spectrum; for practical purposes, though, we typically represent colors using three values.
   1. Why does this work? How do we convert from a continuous power distribution to a color "triple"?
   2. Do any distributions look the same? Why or why not?
   3. When rendering, we typically use this simple representation of color (triples in some color space). When we use complex illumination equations, such as in a modern ray tracer, are the resulting colors "correct" (based on the initial colors and the effects we are simulating with our illumination equations)? Ignore the approximations introduced by any particular lighting model; your answer should focus on the effect of representing color as a triple in some color space.
2. Device independent color
   1. Describe the commonly used approach to specify device independent color, by which we can achieve a common set of colors across a variety of devices.
   2. The standard color system used by device independent color has a number of limitations. One is that the colors space is not perceptually uniform. What does this mean, and what color spaces have been proposed to rectify this problem? What are the limitations of these other spaces?
   3. Even if we use a device independent color specification, there is no guarantee that colors displayed on different devices will actually appear the same. On one hand, colors used in different images may not appear the same. On the other hand, the same images may not appear the same on different devices. Discuss the causes of both of these situations.
3. During the German advance on Paris in 1940, the F rench Army were greatly hampered by the Nazis' effective use of camouflage. By painting their tanks and armored infantry carriers with a green that was carefully matched to the color of the Ardennes fores t, they were able to maneuver entire divisions without being detected. After the war, Baron Reynaud Gaspard de Bouvoir, whose chateau was overrun and briefly occupied, conceived of a remarkably simple idea to foi l such camouflage techniques in the future. His notion wa s to outfit soldiers with strongly colored eyeglasses. Monsieur le Baron reason ed that these glasses would provide its wearer with an a lternative trichromatic vision, enabling soldiers to d iscern between the forest and the painted tanks, whose colors appeared identica l to persons of normal trichromatic vision but whose sp ectral power distributions (SPD) were nearly certainly not identical.
   Is the baron correct? If so, for what k inds of lens coloration would the scheme work? If not, where did he go wrong?Justify your answer.
4. Colorimetry
   1. Why do the CIE XYZ device independent color models use imaginary color primaries X, Y and Z, rather than colors that are visible to a human observer?
   2. What is a color gamut?
   3. The HLS color model is often used instead of RGB because certain color transformations are simpler in HLS than in RGB. Given a color (h,l,s) = (120, 0.4, 0.6) in the HLS color space, describe how would you find the following related colors, and give the color specification for the color:
      • The complementary color?
      • A similar pastel (i.e., a bland color close to gray of (approximately) the same brightness)?
      • Two additional colors to use to create “3D” effects, such as is found in window borders in current window systems (a darker one to use for shadows, a brighter one to use for highlights