Final project: Inverse kinematics

Deadline: May 01 11:30AM
Project Description
In this project, you will formulate an unconstrained optimization to solve an inverse kinematics problem.
Task 1: Given a leg model, solve inverse kinematics to move the handle on the foot to the marker in the space
Task 2: The input to your system is a set of marker trajectories from a motion capture system. Your inverse kinematics solver will produce a set of poses (joint configurations) that match the markers
Requirement
-
•Display the resulting motion sequence (poses)
-
•Compute the error of your solution for each frame (sum of square of positional constraints)
Skeleton code
- IK.zip (2.5 MB) contains the source code as well as the solution files.
-
-external.zip (108 MB) contains 2 folders, one for vl and one for fltk.
-
-After extracting both files, keep them in the same directory.
-
-The project can be run by executing the sln file inside the IK folder.
skeleton code for Mac OSX Lion
- Launch a terminal
- Go to vl directory and type “make”
-
-Go to fltk directory and type “make”
-
-Go to main directory and type “make”
The skeleton code provides basic forward kinematics functionality that allows you to change the pose of the character by adjusting each degree of freedom (DOF). The skeleton code reads in a “skel” file, which defines the body links and joints of the character, as well as the handle positions that match the mocap data (c3d files). Your task is to add inverse kinematics functionality to the skeleton code. First, you need to take some time understanding how the skeleton code works.
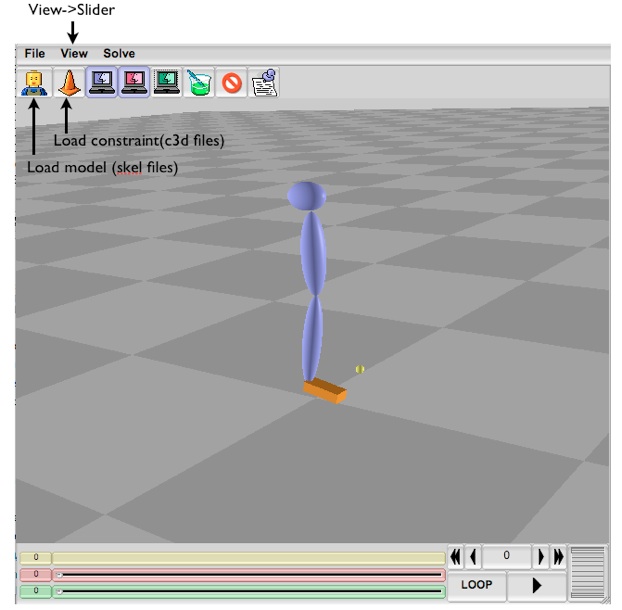
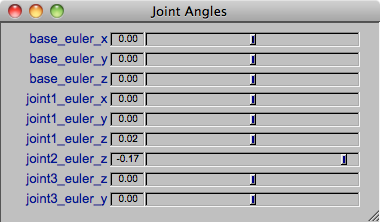
The main window has FLTK widgets that allow you to load a character file and a constraint file (included in the skeleton code). You can manipulate the cameras using the following commands once you load a character.
Shift + left click: rotate
yaw and pitch: move the cursor inside of the yellow circle
roll: move the cursor outside of the yellow circle
Shift + left Ctrl + left click: pan
Shift + left Alt + left click: zoom
The “Joint Angles” window presents the user a set of sliders to adjust the joint angles of the character. You can use them for forward kinematics. Try to load “leg.skel” and “oneMarker.c3d”. Toggle those buttons that have a laptop icon for different choices of visualization. After you are familiar with the UI, restart the program and this time load in “full_body.skel” and “walkRun.c3d”. Hit the “Play” button in the lower right corner of the main window. You should see the marker positions animated on the screen.
Now let’s get into the source code. Where is the entry of the program? The main function (Main.cpp). You realize the only thing the main function does is to activate FLTK interface. So the real entry points of the program are those FLTK callback functions (RealtimeIKui.cpp), which are defined in UICallback.cpp. For example, if we hit the first button with a lego man icon, UICallback::LoadModel_cb() is called. Tracing into that function, LoadModel() in Command.cpp is called, which then instantiates an ArticulatedBody after some file I/O code. Now it is time to examine ArticulatedBody.h and ArticulatedBody.cpp to have a better understanding of how the body links, joint angles, handles, and other information about the character are organized.
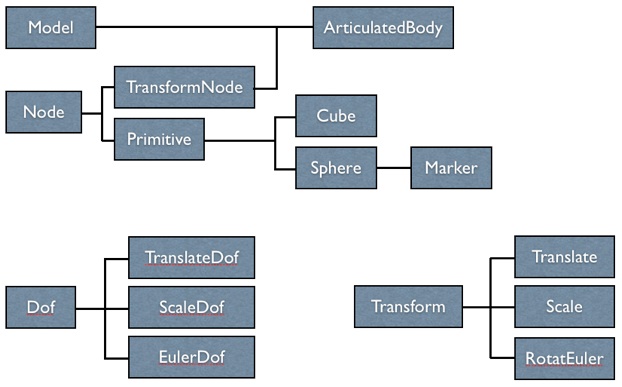
This is an overview of the main classes used to represent an articulated character. We start from ArticulatedBody and its base class Model (Model.h). The data members that require attention are Model::mLimbs, which stores the body links, Model::mDoflist, which stores the information of joints and the current joint angles, and Model::mHandleList, which stores the local coordinates of the handles and their current global coordinates. These three data members belong to three classes: TransformNode, Dof, and Marker.
TransformNode represents a body link. The most important data members are TransformNode::mTransforms, TransformNode::mPrimitives, and TransformNode::mChildren. mTransforms stores the sequence of transformations between this body link and its parent link. For example, the mTransforms for the foot link consists of one translational and two rotational transformations. The translational transformation translates from the origin of the shin to the origin of the foot. The two rotational transformations orient the foot based on the current joint angles of the ankle. The transformation is represented by class “Transform”, which we will examine later. mPrimitives stores the geometry used to represent the body link. Although the data structure allows for multiple geometry associated with a body link, mPrimitives usually only has one member for the characters provided in this project. Each mPrimitive can be instantiated as a cube or as a sphere (there are other types but we can ignore them for now). Finally, let’s look at mChildren. mChildren stores a list of child links associated with this body link. For example, mChildren of the left shin link has only one member, a pointer pointing to the left foot link. Besides these data members, TransformNode also stores the chain of transformations from the root to the current link (mCurrentTransform), the chain from the root to the parent link (mParentTransform), and the chain of local transformations (mLocalTransform). These chains of transformations are very handy when we need to, say, compute the global coordinates of the handle. We only need to update these chains when the the values of DOFs are changed (e.g. the user adjusts the DOF sliders). Storing these chains of transformations speeds up the performance significantly.
Popping one level up, we now look at the class Dof referred by Model::mDoflist. Dof is the base class with three subclasses derived from it: TranslateDof, ScaleDof, and EulerDof (see Translate.h, Scale.h, and RotateEuler.h). Dof stores the current value of the associated joint angle in mVal. This value will be referred by TransformNode::mTransforms to define the current pose of the character.
Model::mHandleList has a list of handles instantiated from Marker class (Marker.h), a very simple subclass derived from Sphere. It stores which body link this handle resides (mNodeIndex), the local coordinates of the handle (mOffset), and the current global coordinates of the handle (mGlobalPos).
Finally, let’s look at the class Transform (Transform.h). Transform has three subclasses: Translate, Scale, and RotateEuler. Each instance of Transform represents a homogeneous transformation associated with a body link. We should pay attention to all the virtual functions in Transform.h. Apply() pushes a transformation matrix into the stack of OpenGL. Each subclass has its own implementation of Apply(). For example, Translate::Apply() calls glTranslated while RotateEuler::Apply() calls glRotated. Apply() is called in TransformNode::Draw(). IsDof() returns a boolean to indicate whether this transformation depends on any degrees of freedom. For example, the translation between the origins of two body links only depends on the bone length, which is not a degree of freedom and its IsDof() will return false. On the other hand, all the rotational transformations involve DOFs that represent joint angles. GetTransform() returns a 4 by 4 matrix of the transformation. This function is used in many places in TransformNode.cpp and ArticulatedBody.cpp. GetDof(int i) returns a pointer to the i-th DOF associated with this transformation. GetDofCount() returns the number of DOFs associated with this transformation. Finally, GetIndex() returns the type of this transformation.
How does the DOF slider trigger the update of the character’s current pose? It all begins with UICallback::DofSliders_cb(). In this callback function, Model::mDofList::SetDof() gets called, which updates the mVal of the DOF and its associated transformation (see DofList::SetDof in Dof.cpp). SetDof() only updates one DOF value and its corresponding transformation. How do we update those chains of transformations of body links and global coordinates of the handles? These updates are triggered by UI->mGLWindow->refresh() in onTimer() in Main.cpp. We can find the definition of this refresh function in PhyterGLWIndow.cpp, which contents only one line: redraw(). We can’t look inside the redraw() function because it is defined by FLTK, but we know that redraw() will trigger the callback function “draw()”, provided by the programmer (i.e. you). So go to PhylterGLWindow::draw() and find the relevant part of the code: if(mShowModel) clause. Continue to trace the code, you will find that TransformNode::UpdateUpMatrix() is called and it updates the transformation chains and global positions of the handles recursively for the entire character.
Besides the data structures for the character, you should also look into C3dFileInfo, a class that stores the desired positions for the handles. Once a C3d file is loaded, you can use GetMarkerPos(int frameIndex, int markerIndex) to query the desired value of a particular handle at a particular time frame. The program will assume the order of handles in Model::mHandleList is the same as the order in C3d file. So it is the user’s responsibility to load a C3d file that matches the current character. If your C3d is a recorded from a motion capture sequence, it is possible that some markers are missing due to occlusion. In that case, C3d will store (0, 0, 0) as the position of the missing marker. If you read in a missing marker at a particular time frame, simply ignore it and not set a constraint on that marker for that time frame.
Your inverse kinematics code should start from Solution() in Command.cpp. This way you can use the button (with green liquid icon) on FLTK UI to trigger your IK program. If you want to access the character in Solution(), you can use UI->mData->mSelectedModel.
Ok. That was a quick tutorial on the skeleton code, but what exactly do you have to do to implement IK solver? You probably have your own way to organize the code, but the following description gives you some pointers to begin. Let’s begin with the objective function:
F(q) = || C1(q) ||2 + || C2(q) ||2 +...+ || Cm(q) ||2
This objective function evaluates the sum of distance between each handle and its desired location. The goal here is to minimize F(q) by modifying q iteratively. We will use gradient descent method to do that. Gradient descent says: at each iteration, compute the gradients of the objective function using current q, move along the negative direction of the gradients for a small step from q, and assign the new position to q.
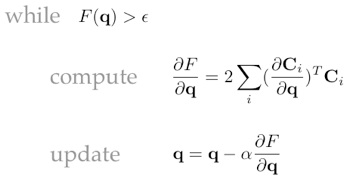
In order to compute the gradients, we need to compute the Jacobian (partial derivative of C with respect to q). The core of this assignment is really about computing the Jacobian. You can put the computation code anywhere you want, but one helpful tip is to implement the derivative computation of each type of transformation (e.g. Translate, RotateEuler) as a virtual function derived from Transform class, similar to Transform::GetTransform(). In fact, the prototype of this function is defined for you in Transform.h.
Mat4d GetDeriv(int dof)
This function should return a 4 by 4 matrix storing partial derivative of the transformation matrix with respect to the DOF which order is indicated by the argument “dof”. You need to implement this function for each of the subclasses derived from Transform.h (namely, Translate, RotateEuler). Now, when you try to compose your Jacobian, all you need to do is call GetDeriv() and GetTransform() for the appropriate body links and DOFs.
Extra credits
-
1.Use quaternion for shoulder and hip joints (HARD)
-
2.Add an objective function G(q) (EASY)
-
3.Add UI (sliders) to control the weight (wi) of each marker (EASY)
-
4.Implement adaptive step size α (EASY)
-
5.Achieve real-time (30 frames per second) (MEDIUM)
-
6.Add playback functionality after solving IK (EASY)