Project 3 / Camera Calibration and Fundamental Matrix Estimation with RANSAC
In Project 3, I was asked to implement the above Camera Calibration and Fundamental Matrix Estimation with RANSAC. This process was easily broken down into three parts listed below./p>
- Camera Calibration
- Estimation of the Fundamental Matrix
- Implementation of RANSAC
Part 1: Camera Calibration
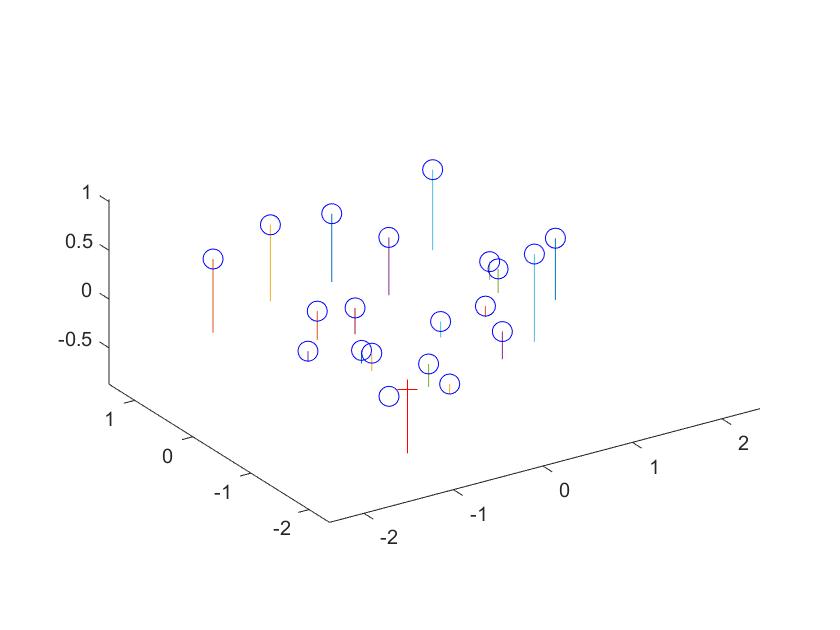
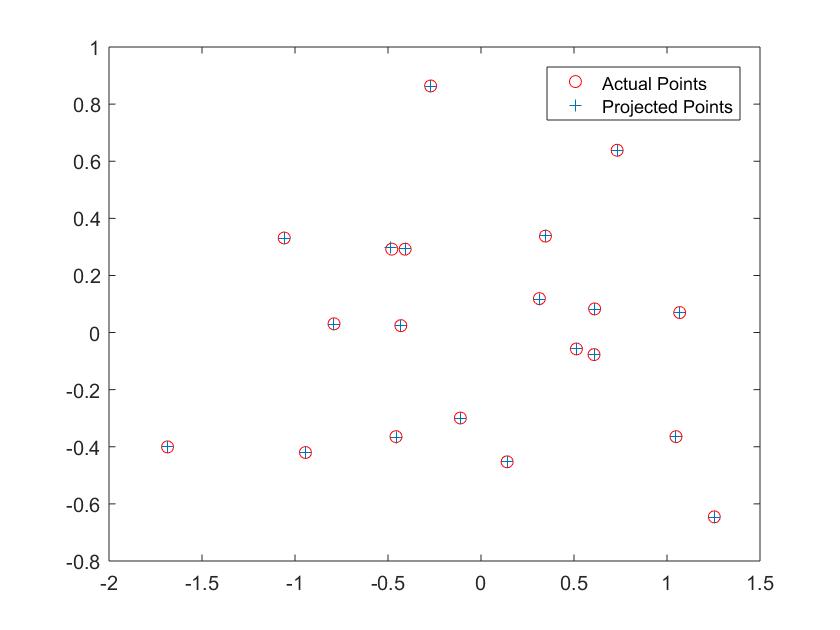
Camera Calibration is broken down into two steps: calculating the projection matrix and then finding the center of the camera. The projection matrix translates the 3D real world coordinates to 2D planar coordinates. Knowing both the 3D and 2D coordinates, one can solve for the projection matrix using a series of linear equations and solving with a regression. Once the projection matrix is found, then one tease out the camera center from the intrinsic K matrix. This is done by treating M (the projection matrix) = [Q|m4], and then solving for the camera center equal to (-Q)^-1 * m4. Below are the results from my code, including the camera center and projection matrix and the code.
%Get current coordinates from Points_2D and Points_3D
n = min(size(Points_2D, 1), size(Points_3D, 1));
for i = 1:n
cur2D = Points_2D(i, :);
cur3D = Points_3D(i, :);
%Create Variables
u = cur2D(1);
v = cur2D(2);
X = cur3D(1);
Y = cur3D(2);
Z = cur3D(3);
linear_equations = [X, Y, Z, 1, 0, 0, 0, 0, -u*X, -u*Y, -u*Z;
0, 0, 0, 0, X, Y, Z, 1, -v*X, -v*Y, -v*Z];
A = [A; linear_equations];
y = [y; cur2D'];
end
M = A\y;
M = [M;1];
M = reshape(M, [], 3)';
%Compute Camera Center
Q = M(1:3, 1:3);
m4 = M(:, 4);
Center = inv(-1 .* Q) * m4;

|
Part 2: Estimation of the Fundamental Matrix
The Fundamental Matrix defines the relationship between the two images coordinated by epipolar geometry around the camera center. The Fundamental Matrix, knowing both the corresponding matches in Image A and Image B, can be solved using a similiar linear regression like the one used to solve for the projection matrix. I specifically used the Singular Value Decomposition to solve for the Fundamental Matrix. Then the matrix rank must be set to 2, so the smallest sigma value in the SVD decomposition should be set to 0. The Fundamental is then recomposed. I also implemented the extra portion that normalizes the points before calculating the Fundamental Matrix. This involves finding the mean values of both A and B and creating respective scale values. Using these values, one can create a Transformation Matrix to normalize the points. This results in a more accurate RANSAC process later down the pipeline. Below are the results of my Fundamental Matrix and the code.
%Extra Credit
meanA = mean(Points_a);
meanB = mean(Points_b);
sumA = 0;
sumB = 0;
for j = 1:n
currentA = Points_a(j, :);
currentB = Points_b(j, :);
sumA = sumA + (currentA(1) - meanA(1)).^2 + (currentA(2) - meanA(2)).^2;
sumB = sumB + (currentB(1) - meanB(1)).^2 + (currentB(2) - meanB(2)).^2;
end
scaleA = sqrt((1/2*n) * sumA);
scaleB = sqrt((1/2*n) * sumB);
for i = 1:n
currentA = Points_a(i, :);
currentB = Points_b(i, :);
%Create Variables (Normalize Homogenous Coordinates)
u = (currentA(1) - meanA(1)) / scaleA;
v = (currentA(2) - meanA(2)) / scaleA;
u2 = (currentB(1) - meanB(1)) / scaleB;
v2 = (currentB(2) - meanB(2)) / scaleB;
linear_equation = [u*u2, v*u2, u2, u*v2, v*v2, v2, u, v, 1];
A = [A; linear_equation];
end
[U, S, V] = svd(A);
%Locate Minimum Sigma
sigmaValues = nonzeros(S);
[value, index] = min(sigmaValues(:));
S2 = S;
S2(index, index) = 0;
F_matrix = U * S2 * V;
F_matrix = V(:,end);
F_matrix = reshape(F_matrix,[],3)';
%Extra Credit - Re-transform F_matrix
TA = [inv(scaleA), 0, -(inv(scaleA) * meanA(1));
0, inv(scaleA), -(inv(scaleA) * meanA(2));
0, 0, 1];
TB = [inv(scaleB), 0, -(inv(scaleB) * meanB(1));
0, inv(scaleB), -(inv(scaleB) * meanB(2));
0, 0, 1];
F_matrix = TB' * F_matrix * TA;


|
Part 3: Implementation of RANSAC
RANSAC consists of three main steps for implementation. Calculating a random subset of k correspondences, estimating an error for each correspondence, then keeping the inliers (those correspondence errors that were below a certain threshold). RANSAC is run thousands of times, and each time the greatest number of inliers (the most accurate fundamental matrix) is retained. At the end of the iterative process, the best numbers are kept and returned. In my code, I ran the RANSAC process 3000 times with a threshold of 0.0001. With the implemented extra credit, the accuracy of each match increased, with almost no spurious correspondences making it past the RANSAC process. Below are the following results for the three test cases and a portion of the RANSAC process.
for i = 1:1000
random_vector = randsample(n, 8);
F = estimate_fundamental_matrix(matches_a(random_vector, :), matches_b(random_vector, :));
tempInliersA = [];
tempInliersB = [];
%Create Current A & B points
for j = 1:n
A = matches_a(j, :);
B = matches_b(j, :);
homogenousA = [A, 1];
homogenousB = [B, 1];
error = homogenousB * F * homogenousA';
if (abs(error) < threshold)
tempInliersA = [tempInliersA; A];
tempInliersB = [tempInliersB; B];
end
end
if (size(tempInliersA, 1) > maxInliers)
maxInliers = size(tempInliersA, 1);
inliers_a = tempInliersA;
inliers_b = tempInliersB;
Best_Fmatrix = F;
end
end



|



|



|



|