Jason Gupta

Project 3: Camera Calibration and Fundamental Matrix Estimation with RANSAC

Part 1: Estimating the Projection Matrix and Camera Center

The first part of this project is calculating the camera projection matrix and then using it to find the camera center. The goal is to compute the matrix that goes from world 3D coordinates to 2D image coordinates. The way that I solved for the projection matrix was setting up a system of equations using the corresponding 2D and 3D points. Once I constructed the matrix representing the system of equations, I used Singular Value Decomposition to solve for the values of our M projection matrix. I was able to confirm my results by computing the residual and making sure it was small. Below is the code accomplishing calculating the projection matrix:

function M = calculate_projection_matrix( Points_2D, Points_3D )
    % create the A matrix for SVD
    A = zeros(size(Points_2D, 1) * 2, 12);
    for i = 1:size(A, 1)
        if (mod(i, 2) == 0)
            A(i, :) = [Points_3D(round(i/2), 1) Points_3D(round(i/2), 2) Points_3D(round(i/2), 3)...
            1 0 0 0 0 Points_3D(round(i/2), 1)*-1*Points_2D(round(i/2), 1)...
            Points_3D(round(i/2), 2)*-1*Points_2D(round(i/2), 1)...
            Points_3D(round(i/2), 3)*-1*Points_2D(round(i/2), 1) -1*Points_2D(round(i/2), 1)];
        else
            A(i, :) = [0 0 0 0 Points_3D(round(i/2), 1) Points_3D(round(i/2), 2) Points_3D(round(i/2), 3)...
            1 Points_3D(round(i/2), 1)*-1*Points_2D(round(i/2), 2)...
            Points_3D(round(i/2), 2)*-1*Points_2D(round(i/2), 2)...
            Points_3D(round(i/2), 3)*-1*Points_2D(round(i/2), 2) -1*Points_2D(round(i/2), 2)];
        end
    end

    [U, S, V] = svd(A);
    M = V(:,end);
    M = reshape(M, [], 3)';
end

After calculating the projection matrix, the final step for part 1 was to calculate the camera center. I did this by using what we talked about in class, taking the last column of our M matrix and using it with the Q (columns 1-3) of our M matrix to calculate our C camera center. The code to do this is below:

function [ Center ] = compute_camera_center( M )
    Q = M(1:3,1:3);
    M4 = M(:,4);
    Center = -1 * inv(Q) * M4;
end

Finally, below are my results from running the first part of the project to confirm that my code performs as expected for the normalized points:

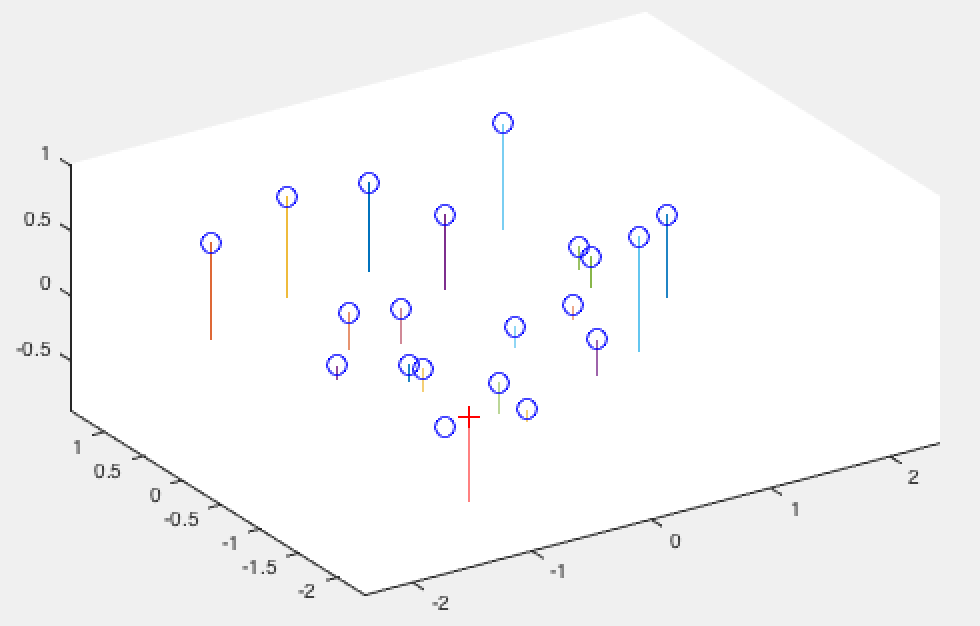
Normalized 3D View

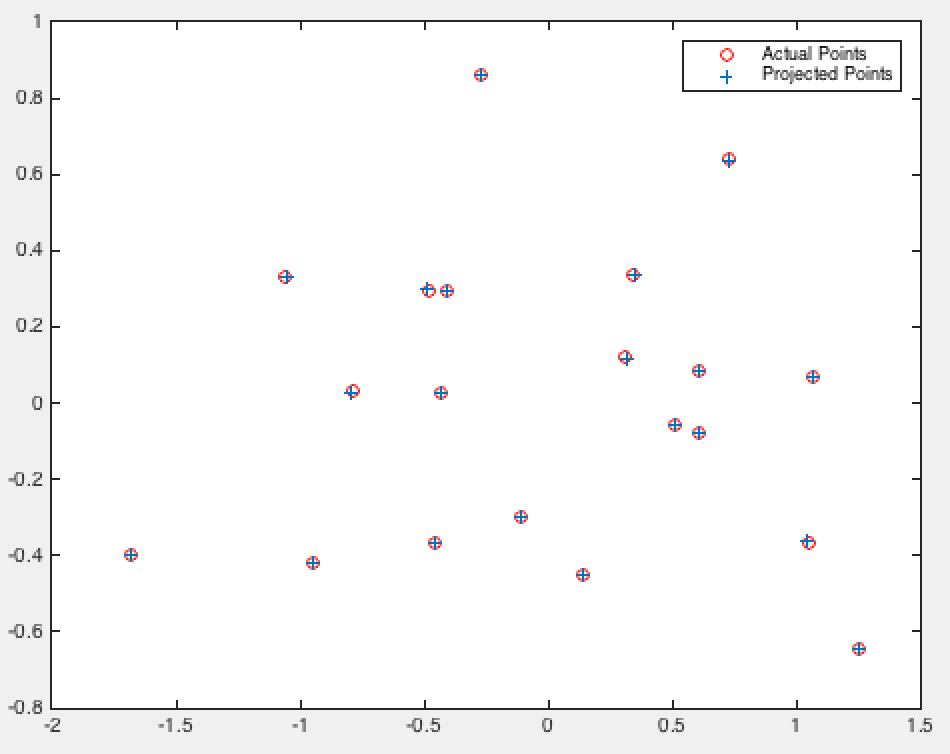
Normalized 2D View

Normalized Matrix, Residual, Camera Center Results

As we can see the camera center is only a rounding error off from the one mentioned in the project description, and our projection matrix is correct!

Part 2: Estimating Fundamental Matrix

For this portion of the project we estimate the fundamental matrix using the 8 point method. Here we do something similar to our first part, however, we set up a different matrix. We create a matrix representing our system of equations and then perform SVD and solve for f where Af = 0. Finally, we resolve det(F) = 0 using SVD once again, finally creating our F fundamental matrix. The code to accomplish this is below:

function [ F_matrix ] = estimate_fundamental_matrix(Points_a,Points_b)
    A = zeros(size(Points_a, 1), 9);
    for i = 1:size(A, 1)
        A(i,:) = [Points_a(i, 1)*Points_b(i, 1) Points_a(i, 1)*Points_b(i, 2) Points_a(i, 1)...
        Points_a(i, 2)*Points_b(i, 1) Points_a(i, 2)*Points_b(i, 2) Points_a(i, 2)...
        Points_b(i, 1) Points_b(i, 2) 1];
    end

    [U, S, V] = svd(A);
    f = V(:,end);
    F = reshape(f, [3 3]);

    [U, S, V] = svd(F);
    S(3, 3) = 0;
    F_matrix = U * S * V';
end

Now let us observe the results on our base image pair (pic_a.jpg and pic_b.jpg).

Pic 1 Epipolar Lines

Pic 2 Epipolar Lines

As we can see, these are exactly the results we want as our epipolar lines align quite well based on the human eye test.

Estimating Fundamental Matrix with Unreliable SIFT matches using RANSAC

The final part of this project focusing on computing the fundamental matrix without perfect point correspondences. Here we use RANSAC to compute the fundamental matrix frmo SIFT point correspondences. Due to outliers we can't use linear regression, so instead we use RANSAC. The jist of this algorithm is we pick 8 points (a number of points I chose) randomly, estimate the fundamental matrix, and determine how well it performs by counting inliers and outliers where an inlier is defined as a point that maintains the properties of our Fundamental Matrix that we know to be true based on some threshold which we define (in this case after trial and error I setted on a threshold of 0.02). We perform this for a reasonable number of iterations (there is a good way to estimate how many iterations are necessary but trial and error showed me that using 2000-4000 iterations was enough to produce good resutls). Finally we return the best fundamental matrix based on the number of points we identified as inliers. Know that the property we speak of with respect to the fundamental matrix is one that says taking point B in homogenous coordinates times F times point A in homogenous coordinates should give us a value of 0. By defining a threshold of 0.02 we are saying that any absolute value below 0.02 is close enough to be considered an inlier, helping to validate our estimated fundamental matrix. The code to accomplish this is shown below:

function [ Best_Fmatrix, inliers_a, inliers_b] = ransac_fundamental_matrix(matches_a, matches_b)
    best_num_inliers = 0;
    inliers_indicies = [];
    for i = 1:4000
        % randomly choose 8 points
        y = randsample(size(matches_a, 1), 8);
        % compute F given these 8 points
        f_matrix_est = estimate_fundamental_matrix(matches_a(y, :), matches_b(y, :));
        % check for all points how many are inliers and how many are outliers
        inliers = 0;
        temp_inliers = [];
        for j = 1:size(matches_a, 1)
            b_vec = [matches_b(j,:) 1];
            a_vec = [matches_a(j,:) 1];
            if (abs(b_vec * f_matrix_est * a_vec') < 0.02)
                inliers = inliers + 1;
                temp_inliers = [temp_inliers j];
            end
        end
        if inliers > best_num_inliers
            best_num_inliers = inliers;
            inliers_indicies = temp_inliers;
            best_matrix = f_matrix_est;
        end
        % keep best answer
    end

    Best_Fmatrix = best_matrix;
    inliers_a = matches_a(inliers_indicies, :);
    inliers_b = matches_b(inliers_indicies, :);
end