Project 3 / Camera Calibration and Fundamental Matrix Estimation with RANSAC
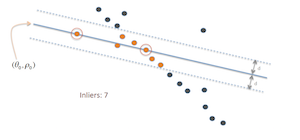
Visual depiction of the RANSAC algorithm for part 3
This project involved implementing much of the math used in practice for stereo and feature matching. The components of this project are as follows:
- Estimating the Projection Matrix
- Estimating the Fundamental Matrix
- Implementing RANSAC to find the best estimate
Projection Matrix and Camera Center
Given a set of 2D and 3D image coordinates, the purpose of this phase of the project was to solve a system of linear equations to calculate the projection matrix and the corresponding camera center. In my approach, I was able to solve for matrix M using linear regression followed by the SVD approach discussed in lecture/the textbook.
My estimation of the projection matrix closely matched the project description:

My total residual was also very low at 0.0445, meaning my estimate was pretty strong.
Lastly, I was able to calculate the camera center by finding:
-Q' * m4, which resulted in a camera center of: <-1.5127, -2.3517, 0.2826>
Implementation
%init
[r, c] = size(Points_2D);
A = ones(2*r, 12);
u = Points_2D(:, 1);
v = Points_2D(:, 2);
u3 = [u, u, u];
v3 = [v, v, v];
APoints_3D = [Points_3D, ones(r, 1)];
A(1:2:2*r, 1:4) = APoints_3D;
A(2:2:2*r, 5:8) = APoints_3D;
A(2:2:2*r, 1:4) = zeros(r, 4);
A(1:2:2*r, 5:8) = zeros(r, 4);
A(1:2:2*r, 9:12) = [-u3 .* Points_3D, -u];
A(2:2:2*r, 9:12) = [-v3 .* Points_3D, -v];
%text-book SVD
[~, ~, V] = svd(A);
M = V(:,end);
M = reshape(M,[],3)';
M = -1 * M;
Fundamental Matrix and Epipolar Lines
For this part of the project, we were asked to estimate the fundamental matrix in a similar manner as part 1. The 8-point algorithm is used to estimate F, followed by SVD and manual altering to estimate a rank 2 version of F. The results of this are incredibly accurate, as shown in the pictures below:

|

|
To generate the above pictures, my estimate for the fundamental matrix was:

Implementation
[r, c] = size(Points_a);
A = zeros(r, 9);
temp = [Points_a(:, 1), Points_a(:, 2), ones(r, 1)];
u3 = [Points_b(:, 1), Points_b(:, 1), Points_b(:, 1)];
v3 = [Points_b(:, 2), Points_b(:, 2), Points_b(:, 2)];
A(:, 1:3) = u3 .* temp;
A(:, 4:6) = v3 .* temp;
A(:, 7:9) = temp;
[~, ~, V] = svd(A);
f = V(:, end);
F_matrix = reshape(f, [3 3])';
%fix rank
[U, D, V] = svd(F_matrix);
D(3, 3) = 0.0;
RANSAC to Find the Optimal Model
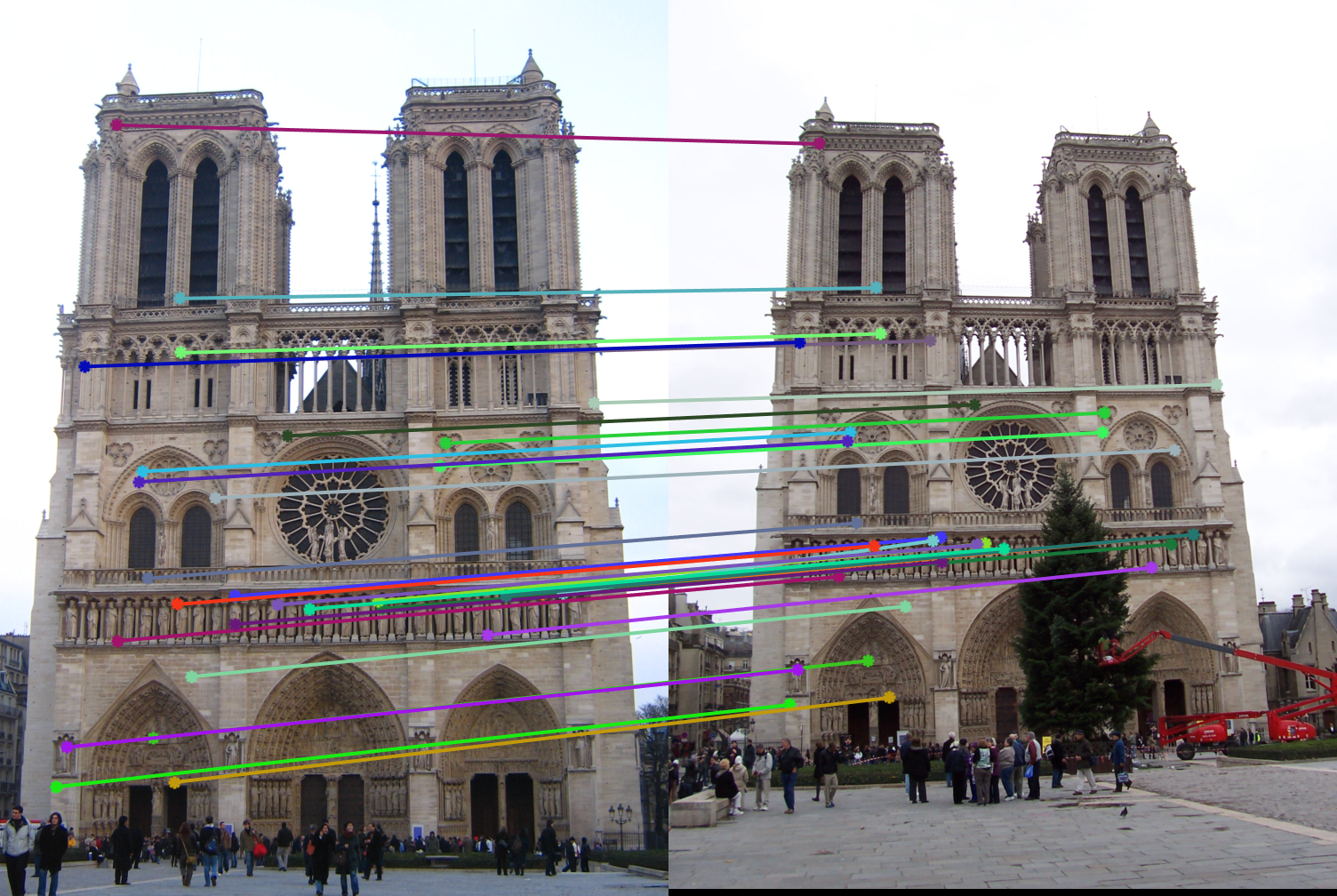
The last part of this project involved using RANSAC to identify strong correspondences from vl_feat's generated matches. With several iterations of RANSAC, I was able to estimate the strongest fundamental matrix parameters such that the greatest number of inliers were achieved. To calculate inliers, I used a threshold of 0.4 and determined if the result from multiplication of the points with the fundamental matrix was less than 0.4 (meaning we fall on an epipolar line). The results of several test images can be seen below:



|


|



|



|
Implementation
[r, c] = size(matches_a);
maxInliers = 0;
Best_Fmatrix = zeros(3, 3);
iterations = 15000;
threshold = 0.04;
numSample = 8;
for i = 1:iterations
points = randsample(r, numSample);
pointsA = matches_a(points, :);
pointsB = matches_b(points, :);
%new model
model = estimate_fundamental_matrix(pointsA, pointsB);
%find inliers
match_a = [matches_a, ones(r,1)];
match_b = [matches_b, ones(r,1)];
currA = zeros(r, 2);
currB = zeros(r, 2);
% no good closed-form way to do this?
for row = 1:r
% Transpose everything so it runs, but is equivalent to the formula
estimate = match_a(row, :) * model' * match_b(row, :)';
if abs(estimate) < threshold
currA(row, :) = matches_a(row, :);
currB(row, :) = matches_b(row, :);
end
end
%get rid of unpopulated rows
currA = currA(any(currA, 2), :);
currB = currB(any(currB, 2), :);
inCount = size(currA, 1);
%Save best model parameters
if inCount > maxInliers
maxInliers = inCount;
Best_Fmatrix = model;
inliers_a = currA;
inliers_b = currB;
end
end
In almost all of the images above, the epipolar lines capture the inliers perfectly. These lead to relatively accurate matches on the test images. However, because normalization wasn't performed the inliers appear slightly off in some of the Notre Dame and Woodruff cases. The lack of normalization made multiple runs of RANSAC rather unstable, leading to slightly inaccurate results. On top of that, inliers that are relatively close to each other also are often missed. It is also worth noting that only 30 points are drawn that were randomly sampled to be inliers - in reality, several more inliers occurred in the chosen fundamental matrix estimation.