Computer Vision Project

Project 3 / Camera Calibration and Fundamental Matrix Estimation with RANSAC

This project is divided into three sections.

Estimating the projection matrix
Estimating the fundamental matrix
Estimating the fundamental matrix with unreliable SIFT matches using RANSAC

Estimating the projection matrix

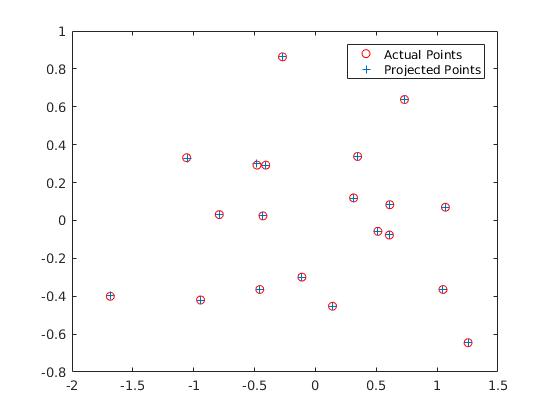
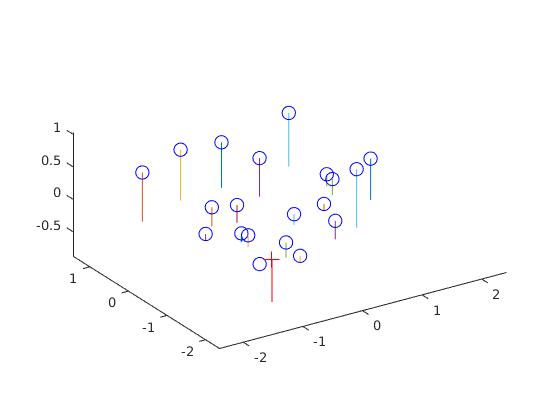
The first part is to calculate the projection matrix from 3D coordinates to 2D image coordinates. We will find our unknown camera parameters from known 3D locations and known 2D image coordinates. I used homogeneous linear system with singular value decomposition. With calculated projection matrix, we can obtain extrinsic parameters such as camera center in world coordinates. Camera center can be obtained with a simple math equation by manipulating parts of projection matrix.

The results are shown below.


The projection matrix is:
   -0.4583    0.2947    0.0140   -0.0040
    0.0509    0.0546    0.5411    0.0524
   -0.1090   -0.1783    0.0443   -0.5968


The total residual is: <0.0445>

The estimated location of camera is: <-1.5127, -2.3517, 0.2826>


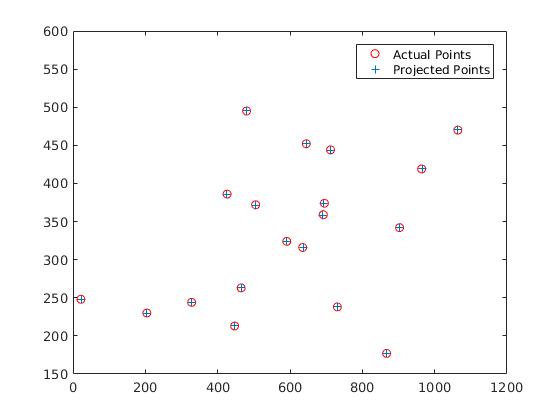
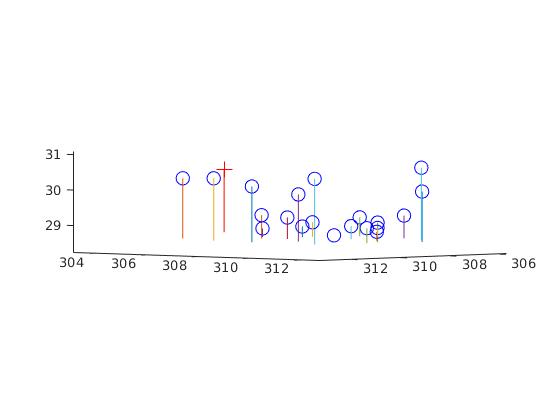
The projection matrix is:
   -0.0069    0.0040    0.0013    0.8267
   -0.0015   -0.0010    0.0073    0.5625
   -0.0000   -0.0000    0.0000    0.0034


The total residual is: <15.5450>

The estimated location of camera is: <303.1000, 307.1843, 30.4217>

Good estimation. Awesome.

Fundamental Matrix Estimation

In this part, we will estimate a fundamental matrix that maps points in one image to lines. This part is similar in the sense that we will use least squares solution using singular value decomposition. I've used an 8-point algorithm which uses SVD on equations from 8 pairs of correspondences. We solve a system of homogeneous linear equation by solving f using singular value decomposition, then also resolve det(F) = 0 constraint using SVD on F, because the fundamental matrix is a rank 2 matrix. Prior to estimating the fundamental matrix, I've also normalized the coordinates, where I made the mean of the points zero and scaled such that I divide by the maximum distance of offset and actual point.

First row - estimation without coordinate normalization
Second row - estimation with coordinate normalization
Third row - estimation with coordinate normalization (with noise)

You can see that not all points lie on epipolar lines well when coordinates are not normalized. However with estimation, we see that all of the epipolar lines cross through the corresponding point in the other image.
Below are corresponding estimated fundamental matrices by row.


[-5.362641983826135e-07,7.903647708579475e-06,-0.001886002040236;
8.835391841159006e-06,1.213216850113133e-06,0.017233290101449;
-9.073822644075863e-04,-0.026423464992204,0.999500091906703]

[-1.622063944941782e-08,2.302245387033617e-07,-5.737507444204410e-05;
1.576534272517726e-07,-4.037388270601488e-08,4.618991730937043e-04;
-4.206880999355947e-06,-6.338606275812155e-04,0.015342462351350]

[-1.746399629535442e-08,2.393093998747028e-07,-6.116164010440586e-05;
1.369154937624769e-07,2.654545969144753e-09,4.586045598953245e-04;
3.346028389409478e-06,-6.523632373120471e-04,0.018463540556430]

Fundamental Matrix with RANSAC

We are going to obtain the fundamental matrix with unreliable point correspondences computed with SIFT. We will find our fundamental matrix with RANSAC, where we will generate multiple fundamental matrices with random sampling of eight coordinates at a time. We will pick the fundamental matrix which scored the best (by the fraction of inliers within a preset threshold). Inlier score is assessed through multiplication of estimated fundamental matrix against coordinates in one image to coordinates in another image. The coordinates with errors less than the threshold is added to the score. In RANSAC, there are few free parameters: number of samples, sampled points, and distance threshold. I chose 8 sampled points, because it is the minimum number needed to fit the model with our 8-point algorithm. Lower sampled points allow us to have smaller number of samples. Number of sampels and distance threshold were tuned to best match a particular image set.

Results

The program outputs many matched points, but I've limited to only 30 for visualization purposes. 30 pairs are chosen at random with the code below in proj3_part3.m file.


randIndx = randsample(size(matched_points_a, 1), 30);
matched_points_a = matched_points_a(randIndx, :);
matched_points_b = matched_points_b(randIndx, :);

The first image shows all SIFT matches, and the second image shows the filtered matches (constrained by 30 for vis). The third and fourth images are epipolar lines and corresponding points.
Mount Rushmore pair does well as expected, because most of the initial matches with SIFT are correct.

Despite SIFTs wrong matches, RANSAC does a very good job with Notre Dame, filtering spurious matches.

SIFT does badly on this image pair. However with RANSAC using normalized coordinates, matching is quiet impressive. In my implementation, I've followed the guidelines set by this assignment rubric by editing the estimate_fundamental_matrix.m. However, RANSAC only passes in 8 sample coordinates. Therefore, to have much better performance, estimate_fundamental_matrix.m should be passed in with more parameter values to account for global mean and distances, instead of sampled mean and distances.