Project 3 / Camera Calibration and Fundamental Matrix Estimation with RANSAC

Example of Epipolar lines on a picture Gaudi.
The purpose of this project was to gain an understanding of camera and scene geometry. The way this was accomplished was by implementing code to find the following
- Projection Matrix
- Fundamental Matrix
- Fundamental Matrix with RANSAC
Projection Matrix
Finding the camera projection matrix can be acheived by solving a system of linear equations with the help of Singular Value Decomposition. The exact methods for this are thoroughly described in the slides so it was very straightforward. A summary as well as a code snippet is shown below.

%Calculating M
[U,S,V] = svd(A);
M = V(:, end);
M = reshape(M, [], 3)';
The results of my estimation were as follows:
The projection matrix is:
[0.4583 -0.2947 -0.0140 0.0040
-0.0509 -0.0546 -0.5411 -0.0524
0.1090 0.1783 -0.0443 0.5968]
The total residual is: 0.0445. The estimated location of camera is: (0.0696, 0.1081, 0.0019)
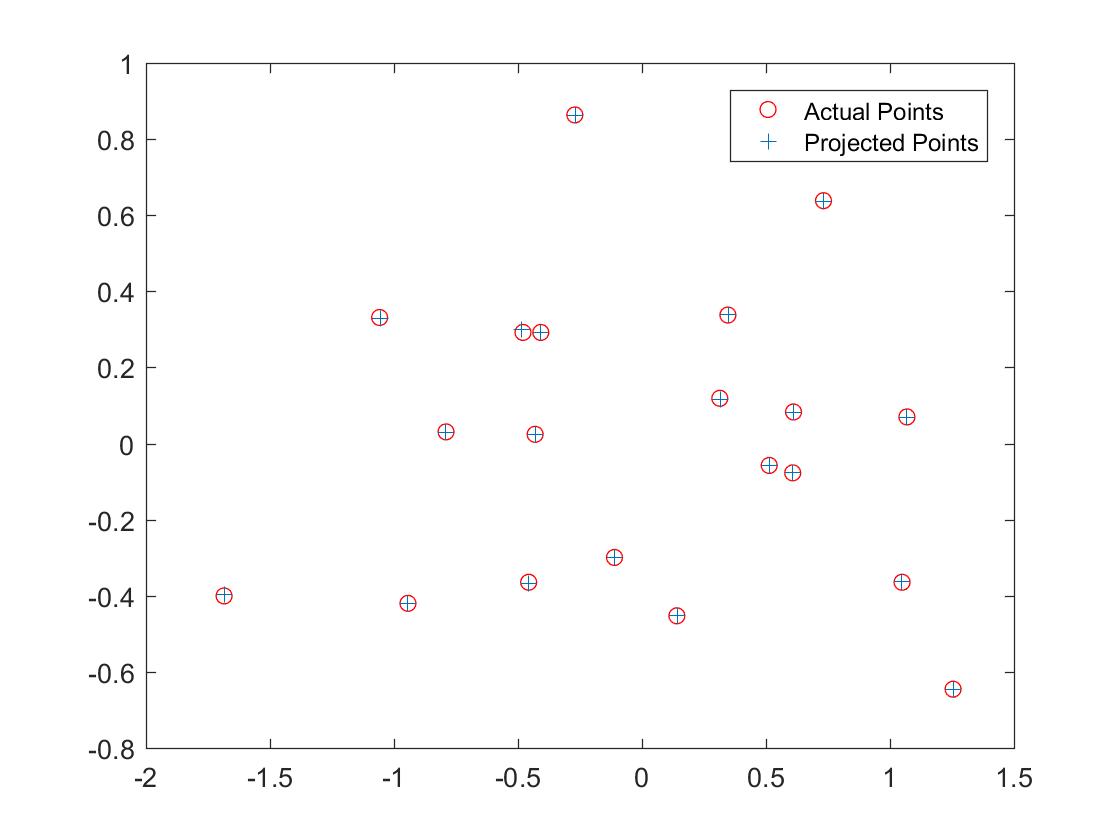
Comparison of actual and projected points after estimating the projection matrix.
Fundamental Matrix
Much like the projection matrix, the fundamental matrix, F, can also be found with a system of linear equations and the use of SVD. However, F has the additional constraint that it's determinant must be zero. Because of this there is some additional code that must be run. The code along with a summary of the linear system of equations is shown below.
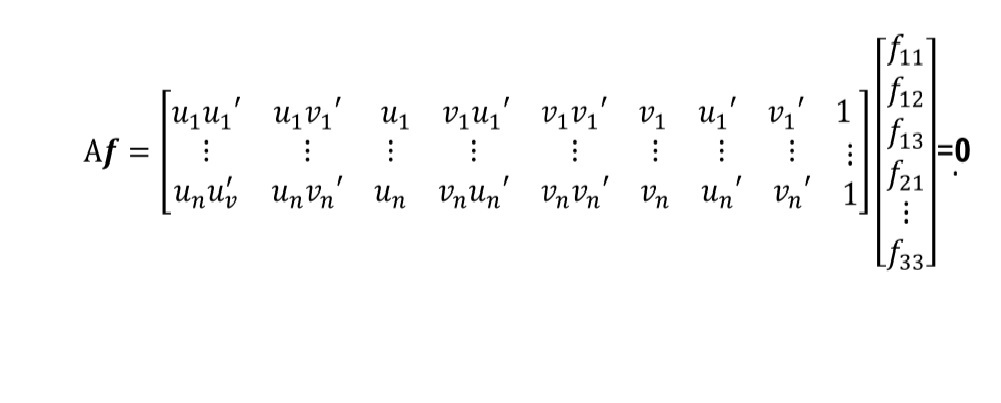
%adding constraint to F
[U,S,V] = svd(F_matrix);
S(3,3) = 0;
F_matrix = U*S*inv(V);
The estimated part 2 F_matrix =
[-0.0000 0.0000 -0.0006
0.0000 -0.0000 0.0045
-0.0000 -0.0062 0.1446]
Part 2 Epipolar Results


|
Using RANSAC to determine Fundamental Matrix
Rather than using all of the points to determine the fundamental matrix, it can be faster and therefore more desirable to pick 8 points at random and use the 8-point algorithm to calculate the F matrix. In order to ensure that these randomly selected points will return the desired result, it is common to iterate through the RANSAC loop a high number of times. In this case, I used 5000 iterations. In each loop, the number of inliers and outliers is determined based on a treshold. In an ideal scenario, XT*fmatrix*X_prime = 0. However, due to noise, that value will almost always be non-zero. The treshold that I used for this value was 0.005. That is to say, if XT*fmatrix*X_prime is smaller than 0.005, then I've found an inlier. At the end of each loop, the number of inliers is counted and if this number is the highest thus far, then we remember the set of inliers as well as the fundamental matrix that corresponds to these points. The result of all these iterations and comparisons is the best possible F matrix for the random points selected. The table below shows the results for all 4 image pairs.



|



|



|



|
For most of these pairs, RANSAC was able to find a set of epipolar lines that crossed through almost all of the feature points. In the Notre Dame set, however, there were a few completely mismatched features as well as features that didn't have an epipolar line going through them. For this reason, the extra credit problem of coordinate normalization was implemented and will be describe in the next section.
Fudamental Matrix with Coordinate Normalization
A method of improving the accuracy of our algorithm is through coordinate normalization. In short, the poor numerical conditions of the pictures that we have been given can be improved by normalizing the coordinates as this effectively reduces the noise cause by rounding errors.


|


|
The table above shows the improvements that were made in calculating the fundamental matrix and finding the epipolar lines for the gaudi image set. As you can see, the images in the bottom row, those with normalized coordinates, have epipolar lines with vanishing points that are much more in line with the horizon and where a human would place a vanishing point for the picture. The epipolar lines in the first row, though they go through all of the feature points, place the vanishing point somewhere in the middle of the castle. The limitations that my algorithm faced with the Notre Dame picture set were much improved with the normalization as can be seen below.


|


|