Raj Prateek Kosaraju

A matched image of Gaudi, after normalization. The lines indicate matched features.

Camera Projection Matrix Extimation

The first goal is to compute the prjection matrix that goes from 3D world coordinates to 2D coordinates. The equation to move from 3D to 2D coordinates is:

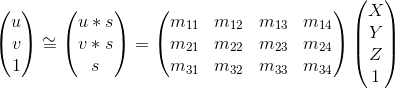
Compute matrix M

Our task is to compute the matrix M. We can set up the linear regression to find the elements of matrix M. Since the resulting equations can have many different solutions, with one of them being unhelpful with M = zeros, we can fix the last element in M to one and solve for the remaining elements of M. This will gurantee that we don't end up with all elements as 0.

Compute center

To compute the center of the camera, we can simply use the below equation:

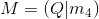
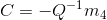
Here, M is made up of a 3x3 we’ll call Q and a 4th column called m_4. The resulting C matrix is the 3D coordinates of the camera center.

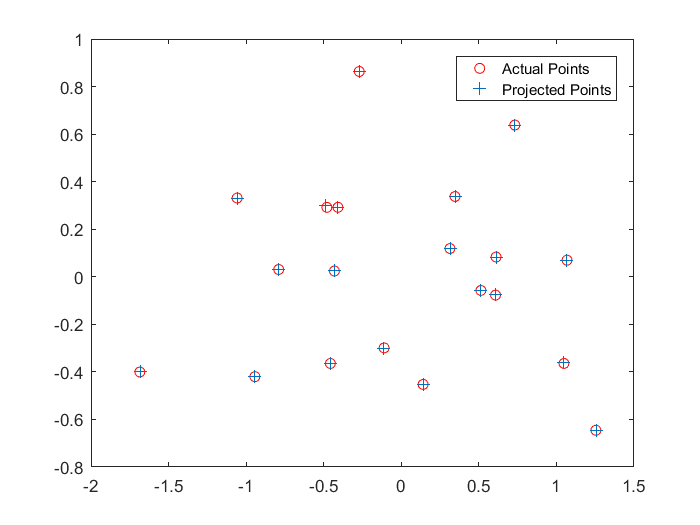
Actual and projected coordinates in 2D for the first set of points.

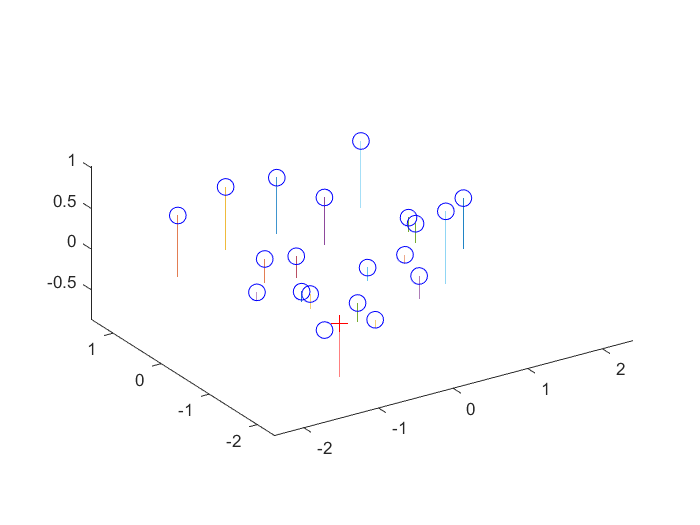
Actual and projected coordinates in 3D with camera center for the first set of points.

Fundamental Matrix Estimation

This part is for estimating the mapping of points in one image to lines in another by means of the fundamental matrix. The fundamental matrix is defined by:

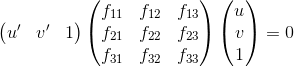
We can set up the regression equations in a similar way to part 1 and solve for matrix F. However, the least squares estimate of F will be full rank, where as the fundamental matrix is a rank 2 matrix. In order to reduce its rank, we can decompose F using SVD and then estimate a rank 2 matrix by setting the smallest singular value in Sigma to 0 and then recomputing F using the new sigma matrix.

First image epipolar lines

Second image epipolar lines

Fundamental Matrix using RANSAC

Now, we will compute the fundamental matrix with unreliable point correspondences computed with SIFT. We will try to estimate the best Fundamental matrix given unreliable corrspondences, using RANSAC.

We first determine the number of iterations we should run for, using the equation discussed for RANSAC. We will then sample points randomly, estimate a fundamental matrix for those points and repeat this iterations number of times. We will chose the fundamental matrix with the max number of inliers, i.e., max number of corresponding points falling within the set threshold.

Below is a code snippet that illustrates how this is done in matlab.

%as discussed in class
threshold_delta = 0.04;
p = 0.99;
outlier_ratio = 0.5;
num_points_to_sample = 8;
iterations = log(1 - p) / log(1-(1 - outlier_ratio) ^ num_points_to_sample);

for sample = 1:iterations
    inliers = 0;
    inliers_a_current = [];
    inliers_b_current = [];
    indices = randsample(1:numPoints,num_points_to_sample);
    sampled_a = matches_a(indices,:);
    sampled_b = matches_b(indices,:);
    F_matrix = estimate_fundamental_matrix(sampled_a, sampled_b);
    for pointNum = 1:numPoints
        distance = abs([matches_b(pointNum, :), 1] * F_matrix * [matches_a(pointNum, :), 1]');
        
        if distance < threshold_delta 
            inliers = inliers+1;
            inliers_a_current = [inliers_a_current; matches_a(pointNum, 1), matches_a(pointNum, 2)];
            inliers_b_current = [inliers_b_current; matches_b(pointNum, 1), matches_b(pointNum, 2)];
        end
    end
    if inliers > max_inliers
        Best_Fmatrix = F_matrix;
        inliers_a = inliers_a_current;
        inliers_b = inliers_b_current;
        max_inliers = inliers;
    end
end

First image epipolar lines	Second image epipolar lines
Matched points

Above & Beyond: Normalizing coordinates

Estimate of the fundamental matrix can be improved by normalizing the coordinates before computing the fundamental matrix. I used the approach as described in the project page. The vital equation to keep in mind while normalizing is as follows:

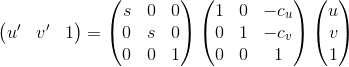
Where s is the scale factor and c is the mean coordinates.

We also have to retrieve the orginal F matrix back while estimating it using:

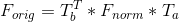
Gaudi: Without normalizing	Gaudi: With normalizing
Notre Dame: Without normalizing	Notre Dame: With normalizing

As we can see from the above results, normalizing seems to have improved the accuracy considerably, espcially in the case of Gaudi.