Computer Vision Project

In this project, we use the geometric relationships between images taken from multiple views to compute camera positions and estimate fundamental matrices for various scenes.

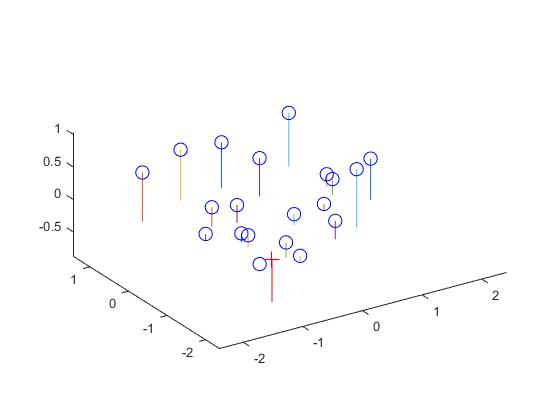
Part I of the project required us to solve for the entries of the 3x4 camera projection matrix that maps 3D coordinates of objects present in a laboratory setting to 2D image points. After computing this camera projection matrix, we could determine the camera's center given these ground truth 3D-2D point correspondences.

Part II is estimating the mapping of points in one image to lines in another by means of the fundamental matrix. For this part of the project, I used Hartley's normalized eight-point algorithm to estimate a least-squares solution of the fundamental matrix parameters.

Part III leverages the VLFeat library to build SIFT feature descriptors around a number of interest points in both images in the stereo pair and takes the input SIFT descriptors to return matches based on the ratio test. In this part, we implement the RANSAC algorithm, which eliminates spurious correspondences found when matching using the ratio test, and combine this method with the normalized eight-point algorithm to estimate parameters for the fundamental matrix containing the greatest number of inliers. The criterion we use to distinguish inliers from outliers is based on a maximum absolute threshold from which an inlying pair of corresponding points (x, x') may not exceed according to the epipolar constraint equation

With RANSAC and the normalized eight-point algorithm, we are able to match corresponding points in both images with ~100% accuracy. Results for Part III are displayed for the Mount Rushmore, Notre Dame, Episcopal Gaudi, and Gaudi image pairs.

In addition, I found a separate image pair taken of the Angkor Wat temple (located in Cambodia) from two different viewing angles, ran the RANSAC algorithm to estimate the best fundamental matrix for these set of correspondences, and obtained reasonably accurate epipolar lines and point matches.

Part I: Camera Projection Matrix

The camera projection matrix

$M=\begin{pmatrix}m_{11} & m_{12} & m_{13} & m_{14} \\ m_{21} & m_{22} & m_{23} & m_{24} \\ m_{31} & m_{32} & m_{33} & m_{34} \end{pmatrix}$

maps homogeneous 3D coordinates to 2D image coordinates as such

$\begin{pmatrix}u \\ v \\ 1\end{pmatrix} \simeq M \begin{pmatrix}X \\ Y \\ Z \\ 1\end{pmatrix}.$

Since we are given 20 ground truth correspondences in pts2d-norm-pic_a.txt and pts3d-norm.txt, we can solve for M by setting up a homogeneous system of 40 equations (2 for each corresponding pair of 3D -> 2D points):

${\begin{pmatrix} X_{1} & Y_1 & Z_1 & 1 & 0 & 0 & 0 & 0 & -u_1X_1 & -u_1Y_1 & -u_1Z_1 \\ 0 & 0 & 0 & 0 & X_1 & Y_1 & Z_1 & 1 & -v_1Z_1 & -v_1Y_1 & -v_1Z_1 \\ . & . & . & . & . & . & . & . & . & . & . \\ X_{n} & Y_n & Z_n & 1 & 0 & 0 & 0 & 0 & -u_nX_n & -u_nY_n & -u_nZ_n \\ 0 & 0 & 0 & 0 & X_n & Y_n & Z_n & 1 & -v_nZ_n & -v_nY_n & -v_nZ_n \\ \end{pmatrix} * \begin{pmatrix}m_{11} \\ m_{12} \\ m_{13} \\ m_{14} \\ m_{21} \\ m_{22} \\ m_{23} \\ m_{24} \\ m_{31} \\ m_{32} \\ m_{33}\end{pmatrix} = \begin{pmatrix} u_1 \\ v_1 \\ \vdots \\ \vdots \\ \vdots \\ \vdots \\ \vdots \\ u_n \\ v_n \end{pmatrix}}$

M has 12 elements, but since the scaling term $m_{34}$ is arbitrary, we only need to solve for 11 variables. Computing the least-squares solution to the system of equations, the projection matrix for the 20 normalized points in Picture A is

$M_{NormA} = \begin{pmatrix} 0.7679 && -0.4938 && -0.0234 && 0.0067 \\ -0.0852 && -0.0915 && -0.9065 && -0.0878 \\ 0.1827 && 0.2988 && -0.0742 && 1.0000 \\ \end{pmatrix}$

Writing M as the concatenation of a 3x3 matrix Q and a column matrix m4 as such

$M = (Q | m_4 )$

we can compute the camera center by solving

$\begin{align*} C &= -Q^{-1} m_4 \\ &= -{\begin{pmatrix} 0.7679 & -0.4938 & -0.0234 \\ -0.0852 & -0.0915 & -0.9065 \\ 0.1827 & 0.2988 & -0.0742 \end{pmatrix}}^{-1} \begin{pmatrix} 0.0067 \\ -0.0878 \\ 1.00 \\ \end{pmatrix} \\ &= \begin{pmatrix} -1.5126 \\ -2.3517 \\ 0.2827 \\ \end{pmatrix} \end{align*}.$

The total residual of this center estimate is 0.0445.

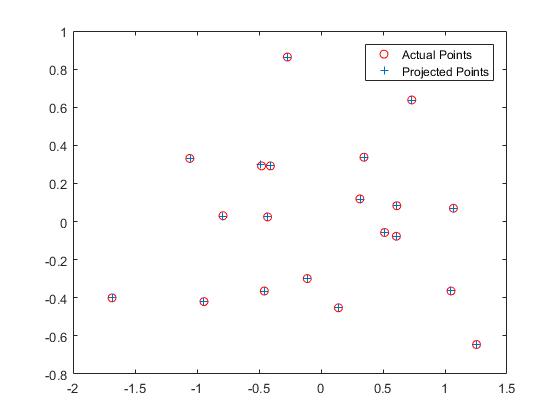Likewise, the camera projection matrix and camera center for Picture B is

$\begin{align*} M_{B} &= \begin{pmatrix} -2.0466 & 1.1874 & 0.3889 & 243.7330 \\ -0.4569 & -0.3020 & 2.1472 & 165.9325 \\ -0.0022 & -0.0011 & 0.0006 & 1 \end{pmatrix} \\ \\ C_{B} &= \begin{pmatrix} 303.0967 \\ 307.1842 \\ 30.4223 \end{pmatrix} \\ \\ Residual &= 15.6217 \end{align*}$

Part II: Fundamental Matrix Estimation

The normalized eight-point algorithm is used to compute the fundamental matrix given point correspondences x = (u, v) and x' = (u', v') in the left and right images, respectively. Each point correspondence generates one constraint on the fundamental matrix F and must satisfy the epipolar constraint equation

$\bold{x'}^TF\bold{x} = 0.$

Expanding the matrices out by multiplication, we obtain the following equation for n point correspondences

$\begin{align*} \begin{pmatrix} u_1'u_1 & u_1'v_1 & u_1' & v_1'u_1 & v_1'v_1 & v'_1 & u_1 & v_1 & 1 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ u_n'u_n & u_n'v_n & u_n' & v_n'u_n & v_n'v_n & v'_n & u_n & v_n & 1 \\ \end{pmatrix} \begin{pmatrix} f_{11} \\ f_{12} \\ f_{13} \\ f_{21} \\ f_{22} \\ f_{23} \\ f_{31} \\ f_{32} \\ f_{33} \end{pmatrix} &= \bold{0} \\ \\ \\ \Leftrightarrow \bold{Af} = 0. \\ \end{align*}$

where A is the n x 9 equation matrix, and f is a 9-element column vector containing the entries of the fundamental matrix F.

From here, the least-squares solution f is easily computed by performing singular value decomposition (SVD) on the matrix A=UDV^T. It is well-known that the vector f that minimizes ||Af|| such that ||f|| = 1 can be found along the column of V corresponding to the least singular value. Next, we rearrange the 9 entries of f to create the 3x3 fundamental matrix F. Then, we perform SVD on F to obtain

$F = U_fD_f{V_f}^T$

We set the smallest singular value of D_f to 0 to create matrix D'_f, thus reducing the rank of the matrix from 3 to 2, and from there we can recompute the rank-2 fundamental matrix as

$F = U_fD_f{V_f}^T.$

Using the version of the eight-point algorithm without prior coordinate normalization to compute the fundamental matrix on the laboratory image pair, we obtain the following fundamental matrix F (truncated to 4 decimal places) and the epipolar lines for both images:

$F_{unnormalized}=\begin{pmatrix} -5.3626*10^{-7} & 7.9036*10^{-6} & -0.0019 \\ 8.8354*10^{-6} & 1.2132*10^{-6} & 0.0172 \\ -9.0738*10^{-4} & -0.0264 & 0.9995 \end{pmatrix} \approx \begin{pmatrix} -0.0000 & 0.0000 & -0.0019 \\ 0.0000 & 0.0000 & 0.0172 \\ -0.0009 & -0.0264 & 0.9995 \end{pmatrix}$

If you look closely, you'll notice that the epipolar lines don't pass exactly through the center of all the point correspondences. How can we improve this?

However, in order to improve the accuracy of epipolar lines generated in Part III, we want to modify the 'vanilla' eight-point algorithm to recenter the point correspondences x_i = (u_i, v_i) and x'_i = (u'_i, v'_i) in both images to their respective centroids before proceeding to compute the least-squares solution for f. After recentering the image points, we must scale the points to be a fixed squared distance from the origin. The coordinate normalization steps can be summarized in the following steps:

Compute the centroid of all corresponding points in a single image:
$\begin{align*} \bold{\bar{u}} &= \frac{1}{n}\sum_{i=1}^{n}{u_i} \\ \bold{\bar{v}} &= \frac{1}{n}\sum_{i=1}^{n}{v_i} \\ \end{align*}$
Recenter by subtracting the mean u and v coordinates from the original point correspondences to obtain
$\begin{align*} \bold{\tilde{u}} = \bold{u} - \bold{\bar{u}} \\ \bold{\tilde{v}} = \bold{v} - \bold{\bar{v}} \end{align*}$
Define the scale term s and s' to be the average distances of the centered points from the origin in both the left and right images:
$\begin{align*} \bold{s} &= \frac{\sqrt{2}}{ \left( \frac{1}{n} \sum_{i=1}^{n}\left({\tilde{u}_i^{2} + \tilde{v}_i^{2}}\right) \right)^{1/2} } \\ \\ \bold{s'} &= \frac{\sqrt{2}}{ \left( \frac{1}{n} \sum_{i=1}^{n}\left({\tilde{u'}_{i}^{2} + \tilde{v'}_i^{2}}\right) \right)^{1/2} } \end{align*}$
Construct the transformation matrices T_a and T_b:
$\begin{align*} T_{a} &= \begin{pmatrix}s & 0 & 0 \\ 0 & s & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix}1 & 0 & -\bold{\bar{u}} \\ 0 & 1 & -\bold{\bar{v}} \\ 0 & 0 & 1 \end{pmatrix} \\ \\ T_{b} &= \begin{pmatrix}s' & 0 & 0 \\ 0 & s' & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix}1 & 0 & -\bold{\bar{u}'} \\ 0 & 1 & -\bold{\bar{v}'} \\ 0 & 0 & 1 \end{pmatrix} \end{align*}$
The normalized correspondence points can be computed from
$\begin{align*} \bold{\hat{x_i}} &= T_a\bold{x} \\ \bold{\hat{x'_i}} &= T_b\bold{x} \end{align*}$
Solve for the fundamental matrix F by applying the eight-point algorithm on the normalized set of point correspondences computed in the previous step.
After obtaining the normalized fundamental matrix F_norm, retrieve the fundamental matrix in the original coordinate frame using the following formula

$F_{orig} = T_{b}^{T} * F_{norm} * T_{a}$

Using the normalized eight-point algorithm on the laboratory image pair, we get

and the fundamental matrix (truncated to 4 decimal places)

$\begin{align*} F_{normalizedPts}=\begin{pmatrix} -0.0000 & 0.0000 & -0.0005 \\ 0.0000 & -0.0000 & 0.0037 \\ -0.0000 & -0.0051 & 0.1192\\ \end{pmatrix} \end{align*}$

Part III: Fundamental Matrix with RANSAC

In practical situations, we will not be given ground truth correspondences between two images, so there must be a way to compute interest points and predict matches between stereo image pairs. We use the VLFeat library to generate SIFT descriptors around detected interest points and assign correspondences based on the nearest neighbor ratio test. In project 2, this method alone produced good results on some occasions, but on other image pairs (most notably the Episcopal Gaudi image set), it failed because there was no way to filter outliers from our results.

We now make use of RANSAC algorithm in tandem with the normalized eight-point algorithm to separate outliers. This addition allows us to estimate the best possible fundamental matrix with the greatest number of inliers.

RANSAC is an iterative algorithm that nondeterministically fits a model to a random sample of points taken from the dataset. As the number of permitted iterations increases, the more likely we are to find a fundamental matrix free of outliers. We can roughly estimate the number of iterations k needed to obtain a solution where some iteration of RANSAC selects only inliers with some probability p, using the following equation:

$\bold{k} = \frac{log(1-p)}{log(1-w^n)}$

where w is the proportion of inliers in the data, and n is the number of points required to estimate the model.

So, for example, if we assume that 50% of the corresponding points returned in the SIFT description and matching phases are inliers, the expected number of iterations to run RANSAC in order to get a sample free of outliers with success probability 99% is equal to

$k = \frac{log(1-.99)}{log(1-.5^8)} \approx 1177$

For a pair of points in a stereo image to be considered a match, it must lie on the same epipolar line as well as satisfy the epipolar constraint. Programmatically, we define an absolute error threshold of .001 such that any pair (x, x') that satisfies the equation

$|x'^TFx| < .001.$

is classified as an 'inlier' in the RANSAC algorithm.

Results

We display up to 35 random correspondences obtained after running RANSAC to compute the fundamental matrix.

Rushmore (unnormalized)

Ran 1000 iterations, error threshold = .001, no coordinate normalization. RANSAC returned 36/825 possible matches in 9.53 secs.

Notre Dame (normalized)

Ran 1000 iterations, error threshold = .001, with coordinate normalization. RANSAC returned 135/851 possible matches in 7.98 secs.

Woodruff (normalized)

Ran 2000 iterations, error threshold = .001, with coordinate normalization. RANSAC returned 52/887 possible matches in 21.94 secs.

Episcopal Gaudi (unnormalized)

Ran 10000 iterations, error threshold = .001, without coordinate normalization. RANSAC returned 76/1062 possible matches in 58.36 secs.

Episcopal Gaudi (normalized)

Ran 10000 iterations, error threshold = .001, with coordinate normalization. RANSAC returned 112/1062 possible matches in 59.06 secs.

Ahh... much better matching accuracy with coordinate normalization!

Angkor Wat (unnormalized)

Ran 1000 iterations, error threshold = .01, without coordinate normalization. RANSAC returned 25/456 possible matches in 9.51 secs.

Angkor Wat (normalized)

Ran 10000 iterations, error threshold = .001, with coordinate normalization. RANSAC returned 189/456 possible matches in 30.03 secs.

Sean Dai (sdai30)

CS 6476: Project 3 / Camera Calibration and Fundamental Matrix Estimation with RANSAC

Overview