Project 3 / Camera Calibration and Fundamental Matrix Estimation with RANSAC

This project involved estimating the camera projection matrix (maps 3D world coordinates to image coordinates), and the fundamental matrix (relates points in one scene to epipolar lines in another).

Part I. Camera Projection Matrix

For moving from 3D world coordinates to 2D camera coordinates, we can utilize this equation:
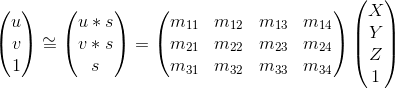
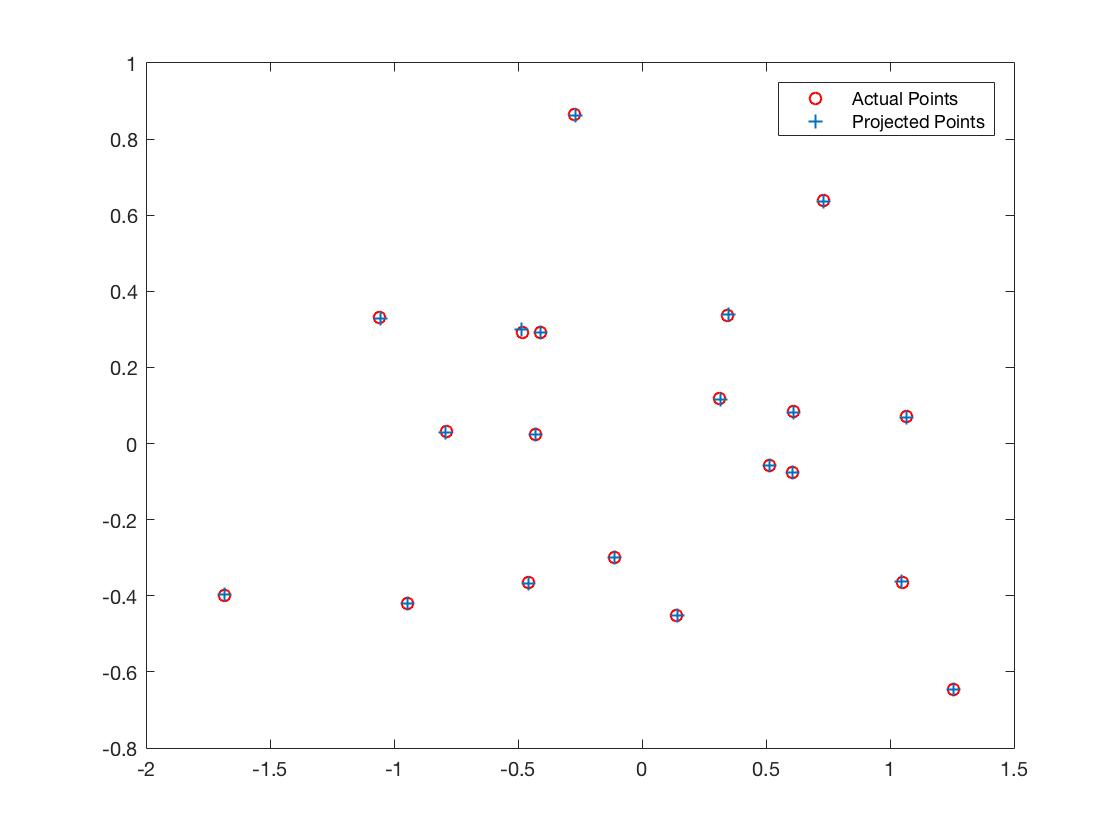
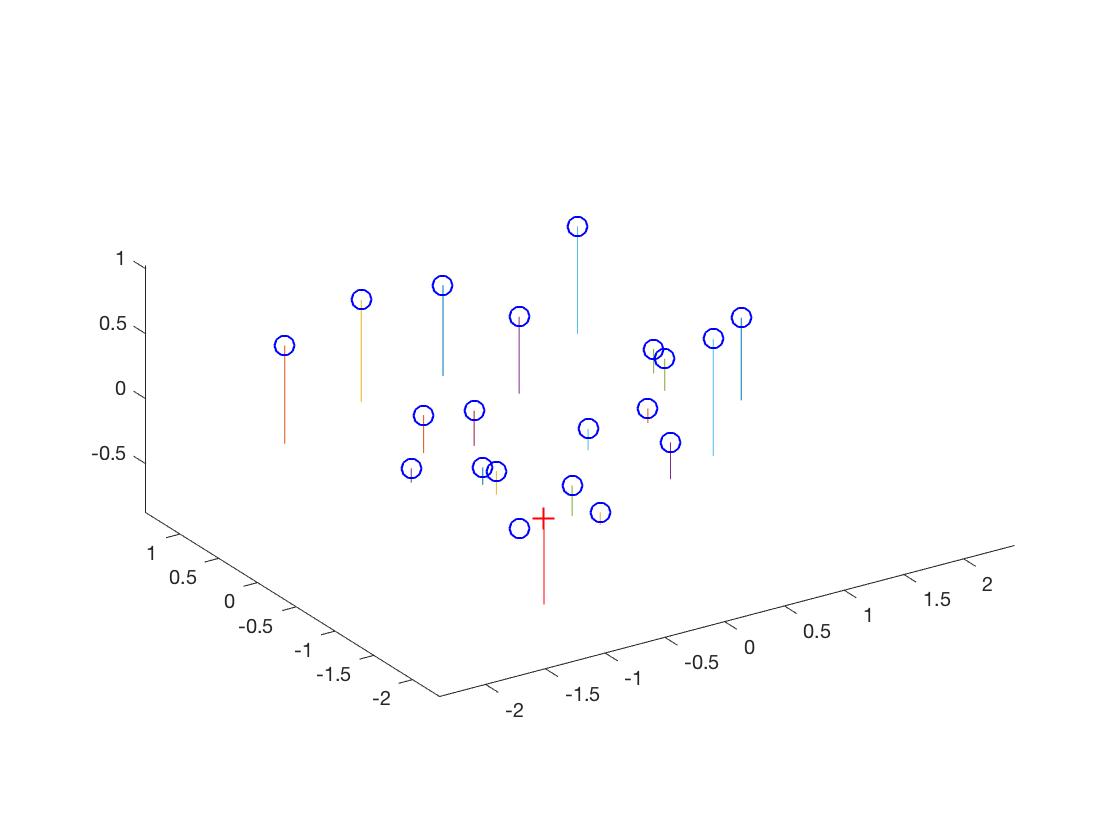
I constrained the last value (m_34) to 1 (to fix a scale), and then solved it using least squares in MATLAB. Here are my results -


MATLAB Code for Camera Projection Matrix


							[size_2d, ~] = size(Points_2D);
							A = zeros(2 * size_2d, 11); % constrain last value for scaling
							B = zeros(2 * size_2d, 1);

							u = Points_2D(:,1);
							v = Points_2D(:,2);
							X = Points_3D(:,1);
							Y = Points_3D(:,2);
							Z = Points_3D(:,3);

							for i = 1:size_2d
							    j = 2 * i;
							    A(j - 1, :) = [X(i), Y(i), Z(i), 1, 0, 0, 0, 0, ...
							                   -u(i)*X(i), -u(i)*Y(i), -u(i)*Z(i)];
							    A(j, :)     = [0, 0, 0, 0, X(i), Y(i), Z(i), 1, ...
							                   -v(i)*X(i), -v(i)*Y(i), -v(i)*Z(i)];
							    B(j -1, 1)  = u(i);
							    B(j, 1)     = v(i);
							end

							% least-squares
							M_init = transpose([A\B; 1]);
							M = [M_init(1:4); M_init(5:8); M_init(9:12)]; % reshape

MATLAB Code for Camera Center


							% Let us define M as being made up of a 3x3 we'll call Q
							% and a 4th column will call m4 :
							Q = M(1:3, 1:3);
							m4 = M(1:3, 4);

							Center = -inv(Q) * m4; % from class

Part II. Fundamental Matrix Estimation

The Fundamental Matrix: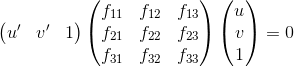
Steps to Estimate: 


						 8-point algorithm
						 1. Solve a system of homogeneous linear equations
						   a. Write down the system of equations
						       uu'f11 + uv'f12 + uf13  + vu'f21 + vv'f22 + ...
						       vf23   + u'f31  + v'f32 + f33    = 0
						   b. Solve f from Af=0 using SVD
						       [U, S, V] = svd(A);
						       f = V(:, end);
						       F = reshape(f, [3 3])`;
						 2. Resolve det(F) = 0 constraint by SVD
						       [U, S, V] = svd(F);
						       S(3,3) = 0;
						       F = U*S*V`;

MATLAB Code for Estimating Fundamental Matrix


							[sizeA, ~] = size(Points_a);
							[sizeB, ~] = size(Points_b);

							A = zeros(sizeA, 9);
							u = Points_a(:,1);
							v = Points_a(:,2);
							u1 = Points_b(:,1);
							v1 = Points_b(:,2);

							for i = 1:sizeA
							    A(i, :) = [u(i) * u1(i), v(i) * u1(i), u1(i), u(i) * v1(i), ...
							               v(i) * v1(i), v1(i), u(i), v(i), 1];
							end


							[U, S, V] = svd(A);
							f = V(:, end);
							F_matrix = reshape(f, [3 3])`;

							[U, S, V] = svd(F_matrix);
							S(3,3) = 0;
							F_matrix = U*S*V`;

Part III. Fundamental Matrix with RANSAC

Point correspondences computed with SIFT are unreliable and noisy. Using least squares to solve for the fundamental matrix will not work well. However, RANSAC is suitable when multiple outliers are present. It has 3 steps -

  1. Sample (randomly) the number of points required to fit the model
  2. Solve for model parameters using samples
  3. Score by the fraction of inliers within a preset threshold of the model
8 points were randomly chosen each time and the fundamental matrix was calculated using these. Then, the number of inliers using the matrix was checked. The threshold for error was 0.05, and the number of iterations were 1500 (1177 are required so that with 8 sampled points and 0.99 probability, atleast one run is free from outliers).

The results:

For the Mt. Rushmore and Notre Dame images, 30 inliers are randomly chosen to be displayed for a cleaner visualization.

MATLAB Code for Estimating Fundamental Matrix with RANSAC 


							num_iterations = 1500; % > 1177
							threshold = 0.005;
							best_num_inliers = 0;

							num_elems = size(matches_a, 1);

							for i = 1:num_iterations
							    rand_indices = randperm(num_elems, 8);
							    rand_a = matches_a(rand_indices, :);
							    rand_b = matches_b(rand_indices, :);
							    F_matrix = estimate_fundamental_matrix(rand_a, rand_b);

							    a_inliers = [];
							    b_inliers = [];
							    num_inliers = 0;
							    for n = 1 : num_elems
							        error = [matches_b(n, :) 1] * F_matrix * [matches_a(n, :) 1]';
							        if abs(error) < threshold
							            a_inliers(end+1, :) = matches_a(n, :);
							            b_inliers(end+1, :) = matches_b(n, :);
							            num_inliers = num_inliers + 1;
							        end
							    end
							    if num_inliers > best_num_inliers
							        best_num_inliers = num_inliers;
							        inliers_a = a_inliers;
							        inliers_b = b_inliers;
							        Best_Fmatrix = F_matrix;
							    end
							end

EC. Normalized Coordinates

I normalized the coordinates using linear transformations: .
The scale was computed by estimating the standard deviation.

MATLAB Code for Coordinate Normalization


							% A:
					    % Mean coordinates
					    A_cu = sum(Points_a(:, 1))/sizeA;
					    A_cv = sum(Points_a(:, 2))/sizeA;

					    % Compute Scale by estimating standard deviation
					    A_s = sqrt((Points_a(:,1) - A_cu).^2 + (Points_a(:,2) - A_cv).^2);
					    A_s = sizeA/sum(A_s); % take mean (sqrt(variance) and reciprocal

					    % Transform Matrix
					    scale = [A_s 0 0; 0 A_s 0; 0 0 1];
					    offset = [1 0 -A_cu; 0 1 -A_cv; 0 0 1];
					    A_T = scale * offset;

					    new_a_points = transpose(A_T * [Points_a ones(sizeA, 1)]');

					    % B:
					    % Mean coordinates
					    B_cu = sum(Points_b(:, 1))/sizeB;
					    B_cv = sum(Points_b(:, 2))/sizeB;

					    % Compute Scale by estimating standard deviation
					    B_s = sqrt((Points_b(:,1) - B_cu).^2 + (Points_b(:,2) - B_cv).^2);
					    B_s = sizeB/sum(B_s); % take mean (sqrt(variance) and reciprocal

					    % Transform Matrix
					    scale = [B_s 0 0; 0 B_s 0; 0 0 1];
					    offset = [1 0 -B_cu; 0 1 -B_cv; 0 0 1];
					    B_T = scale * offset;

					    new_b_points = transpose(B_T * [Points_b ones(sizeB, 1)]');

					    A = zeros(sizeA, 9);
					    u = new_a_points(:,1);
					    v = new_a_points(:,2);
					    u1 = new_b_points(:,1);
					    v1 = new_b_points(:,2);

					    for i = 1:sizeA
					        A(i, :) = [u(i) * u1(i), v(i) * u1(i), u1(i), u(i) * v1(i), ...
					                   v(i) * v1(i), v1(i), u(i), v(i), 1];
					    end

					    [U, S, V] = svd(A);
					    f = V(:, end);
					    F_matrix = reshape(f, [3 3])``;

					    F_matrix = B_T`*F_matrix*A_T;

					    [U, S, V] = svd(F_matrix);
					    S(3,3) = 0;
					    F_matrix = U*S*V';

The results:

Number of inliers changes from 185 in regular to 368 in normalized.

Regular Normalized