Xiaoxi Han

1. Projection matrix and the camera center

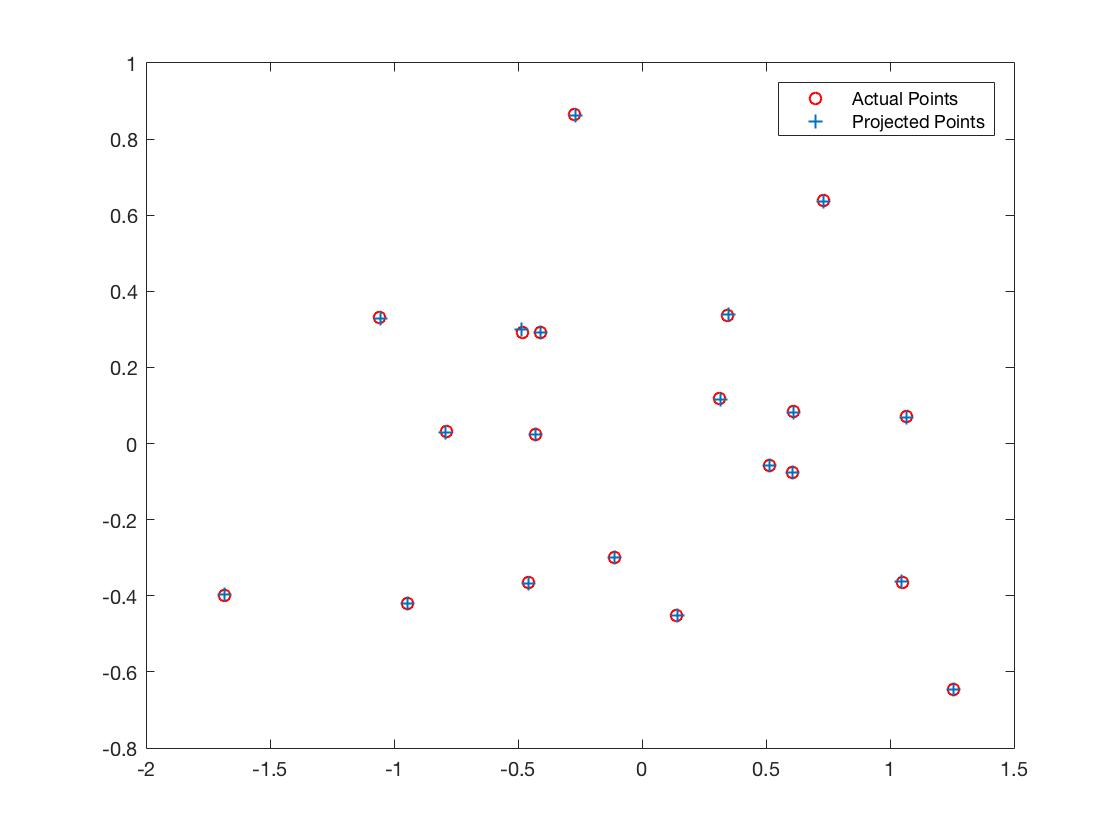
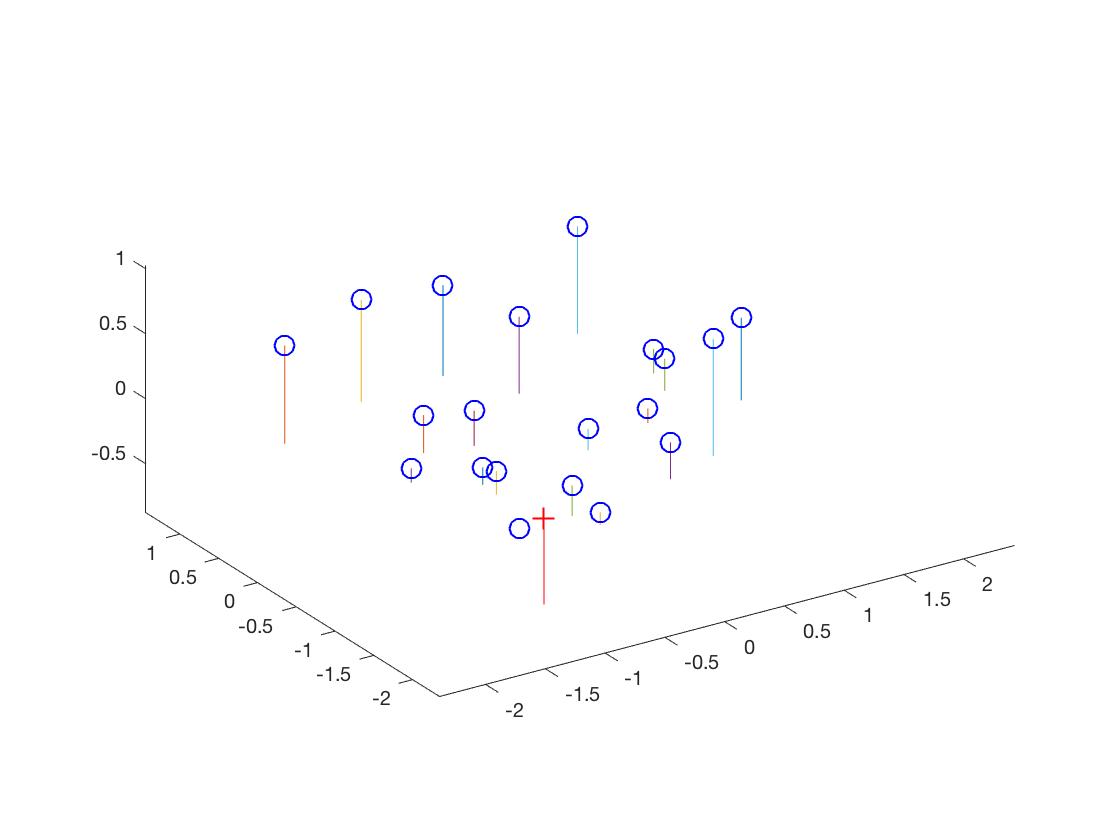
To calculate projection matrix, I used nonhomogeneous linear system and solved for m’s entries using linear least squares. The first image is the projection matrix visualization, and we can see that the projected points are very close to actual points, and the residual is 0.0445, which is very close to 0. And we can see from the second image that the center is also computed correctly, and is located in a coordinate where the camera can catch all the points.

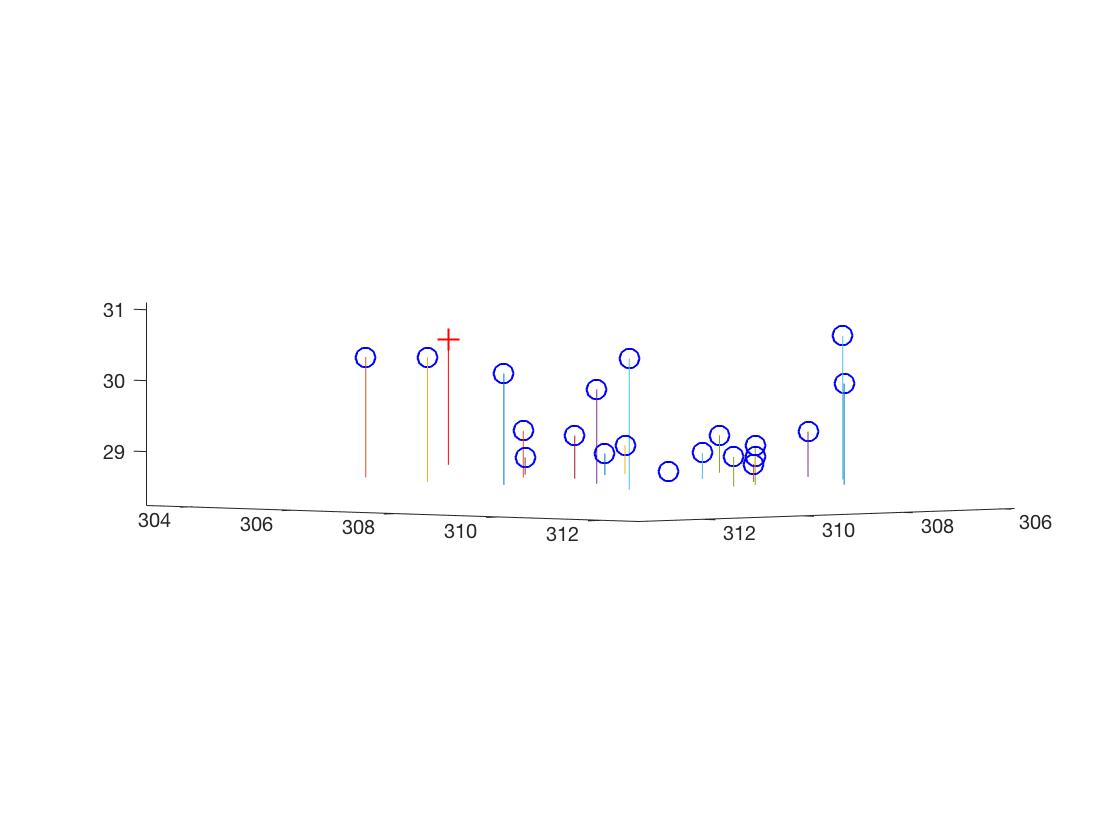
However, when the given points were not normalized, the algorithm had trouble constructing a good projection matrix and camera center. The residual increased to 15.6217, and from the image above we can clearly see that the center is not located in a proper position.

2. Fundamental matrix

To calculate fundamental matrix, I setted up the system of equations using all given matches as following, and fixed the scale of f33 to 1.

[u1u1' v1u1' u1' u1v1' v1v1' v1' u1 v1 1   *   [f11  = [0
 u2u2' v2u2' u2' u2v2' v2v2' v2' u2 v2 1		f12 0
 .......................................	f13	0
 unun' vnun' un' unvn' vnvn' vn' un vn 1]	f21	.
 						f22	.
 						f23	.
 						f31	.
 						f32	.
 						f33]	0]

This way, as shown by the two images above, the fundamental matrix was estimated properly, as we can clearly see all of the epipolar lines crossing through the corresponding point in the other image. I also reduced the rank of the fundamental matrix to 2 by decompose F using svd, assign the smallest singular value to 0, and reconstruct F.

3. RANSAC

When implementing RANSAC, there were several paramenters for me to choose. First is the number of iterations n, which I chose 2000, because from the equation n = log(1-p)/log(1-(1-e)^s), when s = 8, p = 0.99 and e = 0.5, n = 1177, so I choose the number slightly greater than 1177 to make sure that I can consistantly get a good fundamental matrix. And I set the distance threshold to be 0.003, because I found that for all of the image pairs, this threshold can return 100~200 inliers most of the time, which is a relatively good number. With these paramenters fixed, I used eight-point algorithm in each iteration, and finally returned the fundamental matrix with most inliers.

Results in a table

For the Mount Rushmore pair, the algorithm returned 121 pairs of inliers, and we can see from the inlier keypoint correspondences graph that nearly all of the matches are correct.

For the Notre Dame pair, the algorithm returned 90 pairs of inliers, and we can see from the inlier keypoint correspondences graph that again nearly all of the matches are correct. In addition, the matches chosen for this pair are more evenly distributed through the image, generating better epipolar lines than the Mount Rushmore pair.

For the Episcopal Gaudi pair, the algorithm returned 146 pairs of inliers, however there are much more incorrect matches than the first two image pairs. It should work much better if I could normalize the coordinates first.

For the Episcopal Gaudi pair, the algorithm returned 142 pairs of inliers. This pair is easier than the Gaudi pair with fewer incorrect matches.