Project 3 / Camera Calibration and Fundamental Matrix Estimation with RANSAC

RANSAC fundamental matrix
The goal of this project is to get familiar with camera and scene geometry. Specifically we will estimate the camera projection matrix, which maps 3D world coordinates to image coordinates, as well as the fundamental matrix, which relates points in one scene to epipolar lines in another. The camera projection matrix and the fundamental matrix can each be estimated using point correspondences. To estimate the projection matrix (camera calibration), the input is corresponding 3d and 2d points. To estimate the fundamental matrix the input is corresponding 2d points across two images. This project consists of three parts which are listed as follows.
- Camera Projection Matrix
- Fundamental Matrix Estimation
- Fundamental Matrix with RANSAC
Part I
To calculate the camera projection matrix, I applied the least squares regression to solve for M given the corresponding points. Here I set up the nonhomogeneous linear system to find the elements of matrix M. After getting the projection matrix, it is easy to obtain the camera center from the equation C=-Q^-1*m4 .
% code for projection matrix
b = reshape(Points_2D',[],1);
n = size(Points_3D,1);
num_cols = 11;
A = zeros(2*n,num_cols);
zero_pad = zeros(1,4);
for i = 1:n
A(2*i-1,:) = [Points_3D(i,:),1,zero_pad,-Points_2D(i,1)*Points_3D(i,:)];
A(2*i,:) = [zero_pad,Points_3D(i,:),1,-Points_2D(i,2)*Points_3D(i,:)];
end
M = A\b;
M = [M;1];
M = reshape(M,[],3)';
% code for camera center
Q = M(:,1:3);
m4 = M(:,end);
Center = -inv(Q) * m4;
Results
For computing projection matrix, The projection matrix was:
0.7679 -0.4938 -0.0234 0.0067
-0.0852 -0.0915 -0.9065 -0.0878
0.1827 0.2988 -0.0742 1.0000
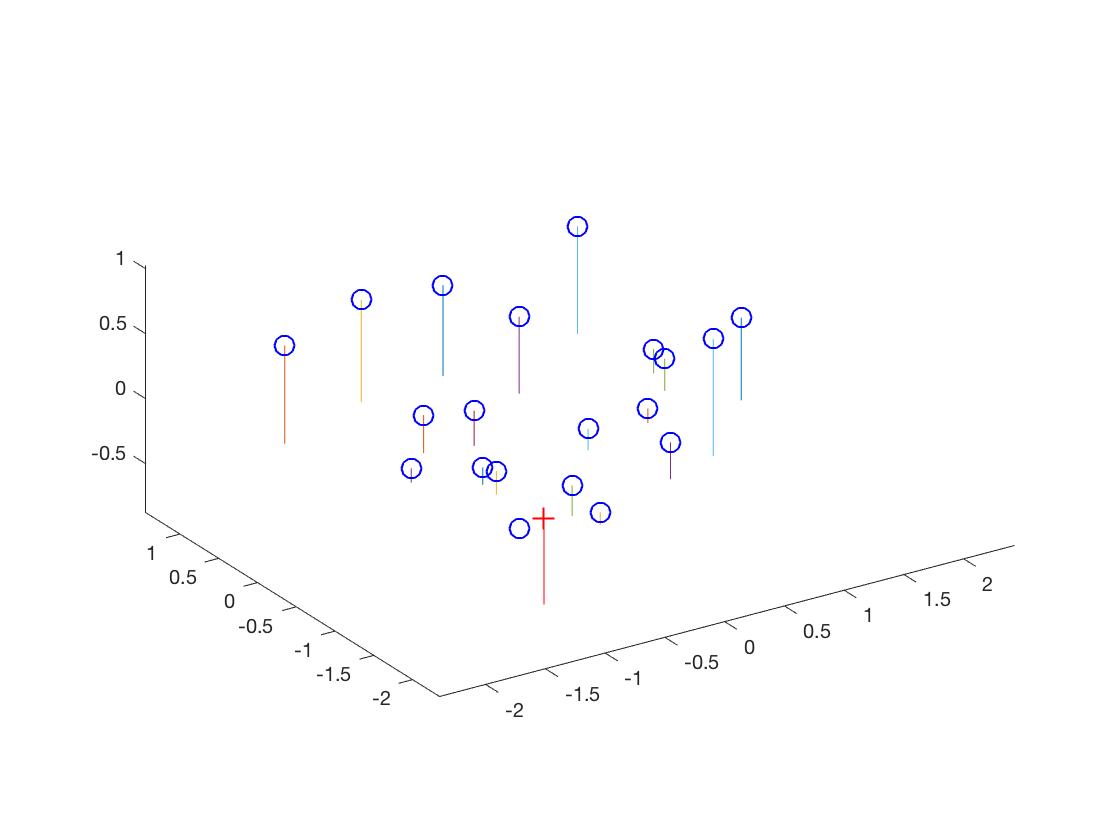
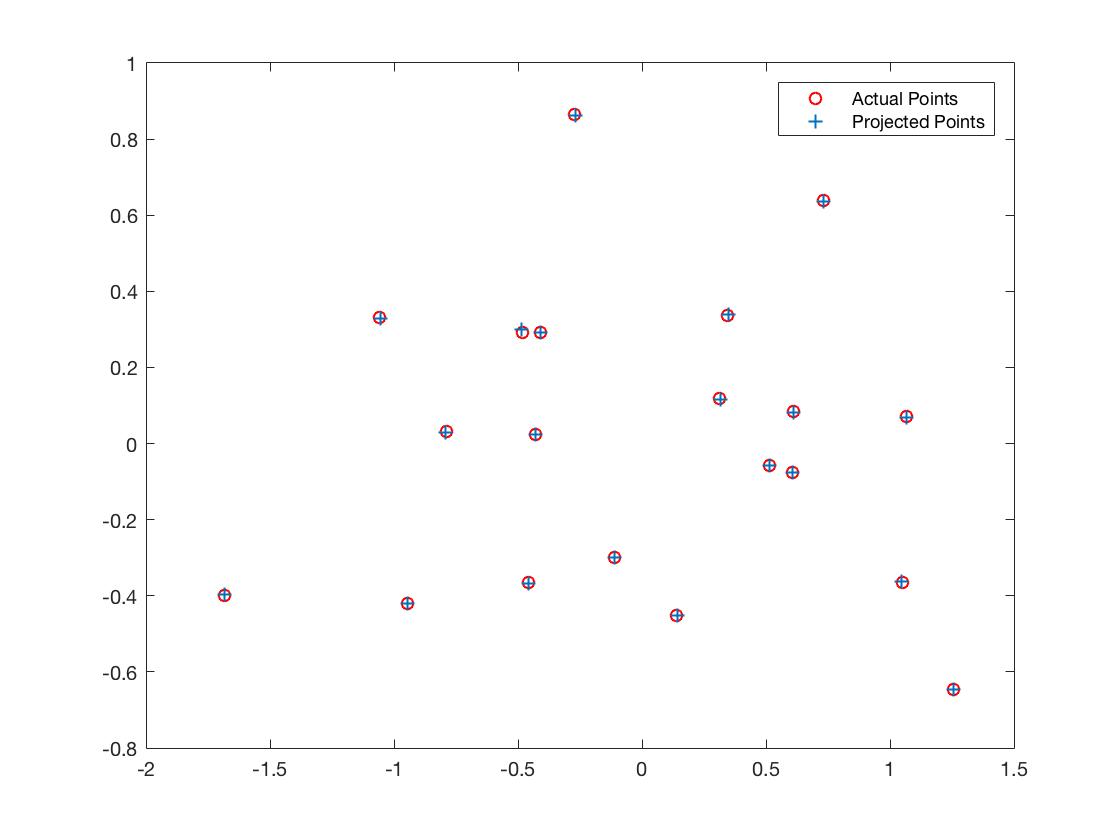
The total residual was <0.0445>, which was quite small. Finally, the estimated location of camera was <-1.5126, -2.3517, 0.2827>. It was almost the same as the expected. Meanwhile, from the chart, we can observe that match projection points quite well with the ground truth points.
|
Part II
To calculate the fundamental matrix, I used a similar approach as mentioned above. First constructing the regression equation and solve it with SVD. We need to pay attention here as the fundamental matrix is a rank two matrix, which means we need to enforce the smallest singular value to be zero.
Extra Credit
For better performance, I implemented normalization when calculating the fundamental matrix. The mean of the two set of points are calculated and I substract the means to center the image data at the origin. Then I estimated the standard deviation of the points and used the reciprocal as the scale factor. After translating and scaling, we have obtained the normalized points. The actual fundamental matrix is recomputed using a formula and returned.
norm_mode = 1;
if norm_mode == 0
n = size(Points_a,1);
num_cols = 9;
A = zeros(n,num_cols);
for i = 1:n
A(i,:) = reshape([Points_a(i,:),1]' * [Points_b(i,:),1],[1,num_cols]);
end
[U,S,V] = svd(A);
f = V(:,end);
F =reshape(f,[3,3])';
[U, S, V] = svd(F);
S(3,3) = 0;
F_matrix = U*S*V';
else
% normalization
n = size(Points_a,1);
num_cols = 9;
Points_a_mean = mean(Points_a);
Points_b_mean = mean(Points_b);
% Points_a = bsxfun(@minus, Points_a, Points_a_mean);
% Points_b = bsxfun(@minus, Points_b, Points_b_mean);
Ta = [1,0,-Points_a_mean(1);
0,1,-Points_a_mean(2);
0,0,1];
std_a = 1/std2(Points_a);
Sa = [std_a,0,0;
0,std_a,0;
0,0,1];
Tb = [1,0,-Points_b_mean(1);
0,1,-Points_b_mean(2);
0,0,1];
std_b = 1/std2(Points_b);
Sb = [std_b,0,0;
0,std_b,0;
0,0,1];
Points_a = [Points_a,ones(n,1)];
Points_b = [Points_b,ones(n,1)];
Points_a_prime = (Sa * Ta * Points_a')';
Points_b_prime = (Sb * Tb * Points_b')';
Points_a_prime = Points_a_prime(:,1:2);
Points_b_prime = Points_b_prime(:,1:2);
A = zeros(n,num_cols);
for i = 1:n
A(i,:) = reshape([Points_a_prime(i,:),1]' * [Points_b_prime(i,:),1],[1,num_cols]);
end
[U,S,V] = svd(A);
f = V(:,end);
F =reshape(f,[3,3])';
[U, S, V] = svd(F);
S(3,3) = 0;
F_matrix = U*S*V';
F_matrix = (Sb*Tb)' * F_matrix * (Sa*Ta);
end
Results
Without normalization, the fundamental matrix is the following:
-0.0000 0.0000 -0.0019
0.0000 0.0000 0.0172
-0.0009 -0.0264 0.9995
With normalization, the funamental matrix turns to:
-0.0000 0.0000 -0.0003
0.0000 -0.0000 0.0027
-0.0000 -0.0037 0.0853
Since all matching points are on the corresponding epipolar lines in both cases. We are not able to observe any difference in part2 before and after normalization.


|
Part III
To estimate fundamental matrix with RANSAC, I repeat the following step for 10000 iterations: randomly pick 9 correspondent point pairs and compute the fundamental matrix, and then count the number of inliers(a threshold 0.002 is applied here). The fundamental matrix which yields the maximum number of inliers is eventually returned.
num_samples = 9;
dim = size(matches_a,2);
sample_a = zeros(num_samples,dim);
sample_b = zeros(num_samples,dim);
inliers_a = [];
inliers_b = [];
[row,col] = size(matches_a);
maximum = 0;
% threshold between inliers and outliers
threshold = 0.002;
num_iterations = 10000;
max_inliers = 100;
for ii = 1:num_iterations
temp_a = [];
temp_b = [];
rand_samples = randperm(row,num_samples);
for i = 1:num_samples
sample_a(i,:) = matches_a(rand_samples(i),:);
sample_b(i,:) = matches_b(rand_samples(i),:);
end
% calculate fundatmental matrix
F = estimate_fundamental_matrix(sample_a,sample_b);
count = 0;
%ransac
for i = 1:row
% count number of inliers
if (abs([matches_b(i,:),1]*F*[matches_a(i,:),1]') <= threshold)
count = count+1;
temp_a = [temp_a;matches_a(i,:)];
temp_b = [temp_b;matches_b(i,:)];
end
end
if(count > maximum)
maximum=count;
inliers_a = temp_a;
inliers_b = temp_b;
Best_Fmatrix = F;
end
end
if size(inliers_a,1) > max_inliers
inliers_a=inliers_a(1:max_inliers,:);
inliers_b=inliers_b(1:max_inliers,:);
end
Results in a table



|



|



|



|



|



|



|



|
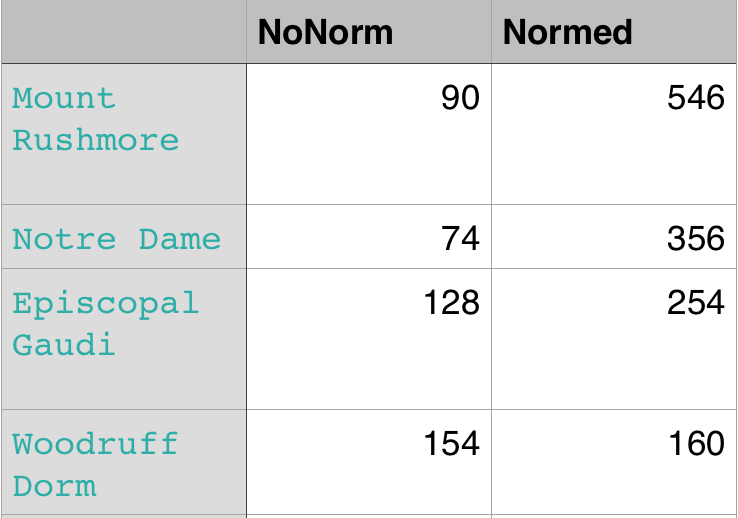
The 1st, 3rd, 5th sets of images are unnormalized points, while the 2nd, 4th, 6th sets of images are figured from normalized points. For unnormalized points, epipole lines do not possess any particular property. However, after normalization, epipole lines are more in order and more precise. Normalization leads to better performance, especially in terms of the number of inliers. The data below shows the number of inliers under same parameters
|