Project 4 / Scene Recognition with Bag of Words
Table of Contents:
- Motivation
- Project Outline
- Confusion Matrix
- No Implementation
- Part 1
- Part 2
- Part 3
- So Far
- Graduate Extra Credit
- Conclusion
- Sources
Motivation:
Our brains make vision easy. It takes minimal effort for us humans to distinct between a leopard and a jaguar. We can read words on signs such as yield and stop and intuitively understand their meaining. We can recognize another human as a human and can classify categories of animals. We are able to understand images. Computers are not able to do what our brains do for us. For a computer to recognize an image we will need to teach it. There are many methods to do this and we will explore two of them:
- Tiny images and nearest neighbor classification
- Bag of quantized local features and linear classifiers learned by support vector machines
At the end of our project, we will be able to classify scenes into 1 of 15 categories by training and testing on the 15 scene database.
Project Outline:
- Part 1: We will implement tiny images representation and then nearest neighbor classifier. Here, we should expect 18-25% accuracy.
- Part 2: We will implement Bag of SIFT representation and run it with the nearest neighbor classifier we built from Part 1. Here, we should expect 50-60% accuracy.
- Part 3: We will implement a linear SVM classifier and run it with the Bag of SIFT representation from Part 2. Here, we should expect 60-70% accuracy.
- Graduate Extra Credit: We will look at vocabulary size, cross validation, the SUN database, and Fisher and will see what our accuracy is and how it has changed.
Confusion Matrix:
We can generate a confusion matrix to visualize how often a test case from category $y$ was predicted to be category $x$. A confusion matrix looks as follows:
The matrix can take on values from 0 to 1, which can be identified through colors in the legend. In our project we will use the "jet" colormap where our spectrum of colors ranges from dark blue to light blue to green to yellow to orange to dark red. In the cart above we see that the diagonal is where we have correct predicted values, i.e. we predict zero to be zero, one to be one, ..., nine to be nine. By examining the legend, we see that the prediction of six being six was highest, as it has a dark shade of red and a value of 0.71. In our case, we will be predicting 15 categories ranging from kitches to forests. If we examine the mean of the diagonal, we can obtain an overall accuracy for all categories in our classification. The higher the overall accuracy, the better our predictions. Ideally, we want the diagonal to be dark red while other squares in the confusion matrix are dark blue. This indicates we have performed good classification. We will see this as we progress from random guessing to k-nearest-neighbors to svm.
We can visualize this even further by creating a table that has the category name, accuracy, sample training images, sample true positives, false positives with true label, and false negatives with wrong predicted label on the $x$ and $y$ axis. This allows us to get a further intuition with what is going on in our program. A sample of this looks as follows:

No Implementation:
Without implementing anything in our project, we will randomly guess the category of each test image. There are $15$ categories, so we have a $\frac{1}{15}$ chance or $\sim 6.67%$ chance of classifying the correct scene. Clicking the button below will pull up the results.
Guessing randomly, we see that we have an overall accuracy of $7.0$%, which is expected based on the probability we described above. Nothing has been implemented in this scenario, let us move forward and make some implementations to see how accuracy progresses in our classification.
Part 1:
Tiny Images: Tiny features were inspired by the simple images used as features in the 80 million tiny images data set for non-parametric object and scene recognition as shown below:

Tiny images are the baseline for our classification system. As they are trivial to implement, they help give us an intuition for the difficulty of the task and types of things that features need to latch onto to make scene classification decisions.
To create our tiny features we want to resize the original image to a very small square resolution such as 16 x 16.
- Parameters: image_paths is an N x 1 cell array of strings where each string is an image path on the file system.
- Return: image_feats is an N x d matrix of resized and vectorized tiny images.
- Setup Variables: We let s be the number of rows in image_paths, row and col be the dimensions of our small square (16 x 16), and our dimension d be row*col.
- For Loop: We iterate over s and read in the image then resize it to the size of our square. We then reshape it into a 1 x d vector. We then append this vector to image_feats.
- Normalization: If we want to let the tiny images have zero mean and unit length then we can take image_feats 1 x d vector and subtract the mean and divide by the standard deviation. This occurs in the for loop.
Let us look at the output if we let our feature be tiny features with and without normalization:
| Style | Accuracy |
|---|---|
| Not Normalized | 6.9% |
| Normalized | 8.4% |
We see that normalization gives us a slight boost in performance, however we are still randomly guessing categories. Normalization should help us marginally as we progress from random guesses to k-nearest-neightbors to svm. So, we will move forward with normalized tiny features. Let us now move forward with implementation of the nearest neighbors classifier.
Nearest Neighbor Classifier: K-nearest neighbor is a non-parametric method used for classification as well as for regression. In our purposes we will use the knn algorithm for classification. With knn classification, the output is a class membership. An object is classified by a majority vote of its neighbors, with the object being assigned to the class most common among its k nearest neighbors. K-nearest neighbors is a simple algorithm that stores all available cases and classifies new cases based on a similarity measure, or distance function. Some common distance measures are the euclidean distance, manhattan distance, and the minkowski distance. This nearest neighbor algorithm requires no training, can learn arbitrarily complex decision boundaries, and it trivially supports multiclass problems. It is quite vulnerable to training noise, though, which can be alleviated by voting based on the K nearest neighbors. Nearest neighbor classifiers also suffer as the feature dimensionality increases, because the classifier has no mechanism to learn which dimensions are irrelevant for the decision. The algorithm is as follows:
- For each training example $(x,f(x))$, add the example to the list of training examples. We need to store the entire list of training examples.
- Query the data point $x_q$, the point with which we want to classify. Let $x_1,x_2,...,x_k$ denote the $k$ instances closest fo the data point $x_q$.
- Return the class that is most frequent among the $k$ instances.
We can depict this graphically as follows:

Let us now implement knn in nearest_neighbor_classify.m:
- Parameters: train_image_feats is an Nxd matrix where d is the dimensionality of the feature representation, train_labels is an Nx1 cell array where each entry is a string containing the ground truth category for each training image, and test_image_feats is an Mxd matrix where d is the dimensionality of the feature representation.
- Return Variable: predicted_categories is an Mx1 cell array, where each entry is a string indicating the predicted category for each test image.
- Setup Variables: We define the follwing variables: Metric, k, X, and Y. Metric is a distance metric that will be used in vl_alldist2. k is the number of nearest neighbors we are examining. X is the transpose of test_image feats. Y is the transpose of train_image_feats.
- Distance: We use vl_alldist2 with parameters X, Y, and Metric. This will give us the variable D, which contains the distances between all elements. We then sort D by row and store the indices in the Variable I. We then resize I by truncating the first k columns.
- predicted_categories: We create the predicted_categories variable which is initially an empty cell. This cell will hold all our final preicted categories.
- Nested For Loop: We iterate from i over the number of rows in I and iterate j over k. We create an empty temporary cell outside our nested for loop. Inside the nested for loop we take I(i,j) and extract the label from it. We then turn this into a string and append it to our temporary cell. We do this for each column in the ith row. We then use the built in matlab function unique to retrieves the string map and unique_strings. We can check if there are no duplicates if the size of the string map is the same size as the temporary cell. If there are no duplciates we will take the predicted category of the first column (k=1) and append it to the cell predicted_categories. If there are duplicates then we will use mode and take unique_strings(mode(string_map)) to find the most common category amongst the k columns in the row. We will then take this most common string as our predicted category in the cell predicted_categories.
- Transpose: Our predicted_categories variable will now have dimension 1xM, so we can simply transpose it and return predicted_categories.
Now, that we have implemented k-nearest neighbors the next natural question is what distance measure do we use and what k value do we use to get the highest accuracy. There are sophisticated methods to discover the optimal k-value, such as cross validation; however, we can run a simple test with a few different distance metrics against different k values and examine the accuracy. We will choose the distance measure that has the best accuracy for the k value. We want to look for an elbow in the graphs we generate. We will chose the maximum k value where peformance starts to not improve. Vl_alldist2 allows the following distance measures:
- LINF: $\text{max} |X-Y|$
- L2: $\text{sum} (X-Y)^2$
- L1: $\text{sum} |X-Y|$
- L0: $\text{sum} (X ~= Y)$
- CHI2: $\text{sum} \frac{(X-Y)^2}{(X+Y)}$
- HELL: $\text{sum} (X^{.5}-Y^{.5})^2$
Where the exponent and division is element-wise.
The accuracys corresponding to k are as follows with k-nearest neighbors and tiny images :
 LINF |
 L2 |
 L1 |
|---|---|---|
 L0 |
 CHI2 |
 HELL |
Examining the above plots, we see that we get the best accuracy with the distance metric CHI2 and with a k value of 3 with the tiny images. This gives us an accuracy of 22.8%. We note that we get similar slightly smaller accuracy values around 21% with the best k for L2, L1, L0, and HELL. LINF gives us the worst accuracy. We will proceed with the CHI2 distance metric and a k value of 3.
The confusion matrix and informative table can be viewed by clicking the button below:
Our baseline scene recognition pipeline, tiny images and nearest neighbors, is much better than the 7% accuracy obtained through random guessing. However, we can move on to a more sophisticated image representation, bags of quantized SIFT features. Let us do this next.
Part 2:
Vocabulary of Words: The bag of words model is a simplifying representation used in natural language processing and information retrieval. Here, a text is represented as the bag of its words, disregarding grammar and word order, but keeping multiplicity. This can be use for image classification in computer vision by treating image features as words. The bag of visual words is a vector of occurence counts of a vocabulary of local image features. The vocabulary of visual words will be the first step we need before we can represent our training and testing iamges as bag of feature histograms. To establish a vocabulary of visual words we will form a vocabulary by sampling many local features from our training set and then cluster them with kmeans. We will then return the cluster centers.
Our implementation of build_vocabulary is as follows:
- Parameters: image_paths is an Nx1 cell of array image paths and vocab_size is the size of the vocabulary
- Return Variable: vocab will be a vector of dimension vocab_size x 128. Here, each row is a cluster centroid/visual word.
- sifts: We start by creating an empty matrix called sifts.
- For Loop: In our for loop we iterate over the number of rows in image_paths. We read in each image_path and turn it to a single data type. We then compute our locations and sift_feats by utilizing vl_dsift with our image and a step size. The smaller the step size the more dense the sampling. Using a step size of 3 will be great for our purposes. We then let our sifs vector be [sifts sift_feats]
- Single: We exit the for loop and turn our sifts vector into a single, just so that we have no data type problems later on.
- k means: We then use vl_kmeans with sifts and our vocab size.
Note that the above process takes 62.44566465 minutes to run. We can decrease the time taken by:
- Larger Step Size: A step size of 3 is small. We could use a larger step size, say 9 or 10. However, this would decrease the density of our sampling.
- Fast: We could use the fast parameter in vl_dsift. This uses a piecewise-flat, rather than Gaussian, windowing function. While this breaks exact SIFT equivalence, in practice is much faster to compute.
- Parfor: We could use a parallel for loop. This will allow us to break up the cpu on our machine and use multiple cores, unlike a regular for loop which just uses one core at 100%. However. some tweaks to the code need to be made to ensure proper rules of parallel processing is followed.
However, once we compute the vocabulary.mat, we will store it so we do not need to recompute it each time we run our project.
Let us now proceed to implementing get_bag_of_sifts.m:
- Parameters: image_paths is an N x 1 cell array of strings where each string is an image path on the file system.
- Return Variable: image_feats is an N x d matrix, where d is the dimensionality of the feature representation. Here, d will equate to the number of clusters or equivalently the number of entries in each image's histogram ('vocab_size').
- Load Vocab: First we load the vocabulary that we built in build_vocabulary.m.
- Initialize image_feats: We then initialize an empty matrix for image_feats, which is our return variable.
- For loop: We iterate over the size of the rows of the image_paths. We first read in every image_path and turn it to a single data type. We then use vl_dsift on this image. We will use the parameter 'fast' and a step size of 8. We will examine the change in these parameters later. The parameter fast uses a piecewise-flat instead of a Gaussian windowing function. This is more an approximation of a SIFT, but runs very quickly. After computing this, we will get our sift_features. We can then cast these as a single to ensure there are no problems with data types and run vl_alldist2 with sift_features and the transpose of our vocab. We have to transpose our vocab because we need agreement in dimension with our sift_features. We then transpose the matrix we get from our vl_alldist2 matrix and let the index be the minimum value in this matrix. We can now compute a histogram using matlab's built in function histc on the index and 1:vocab_size. We will then take this histogram and perform element wise divide with the norm of this histogram, which will be appended into image_feats.
Let us now compare our accuracy with and without the 'fast' parameter, the step size and the time taken to run the program (note the vocab_size = 200 here):
| 'fast' | Step Size | Accuracy | Time |
|---|---|---|---|
| Yes | 10 | 53.6% | 124.886461 s |
| Yes | 8 | 56.4% | 178.570186 s |
| Yes | 5 | 59.2% | 438.831639 s |
| No | 10 | 54.3% | 267.982072 s |
| No | 8 | 56.7% | 322.848910 s |
| No | 5 | 59.2% | 591.709452 s |
Looking at the table above, we see that we achieve a top accuracy of 59.2% with and without the 'fast' parameter. However, the computational expense was very high. The graphs for our top accuracy of no 'fast' parameter and a step size of 5 are displayed through the button below:
However, for slightly less accuracy and much less computational expense, we can use the 'fast' parameter and a step size of 8. The charts for this are shown below:
Using a step size of 3 with and without the 'fast' parameter will give us great accuracy; however, the computational expense is very high. Thus, based on reasonable speed, we get the best accuracy with the 'fast' parameter and a step size of 8 giving us 56.4% accuracy. This is within our target range of 50-60% accuracy. We will use this in our implementation going forward.
Let us now move onto part 3: Linear SVM Classifier.
Part 3:
Linear SVM Classifier: A support vector machine (SVM) is a supervised machine learning algorithm which can be used for classification. With this algorithm, we plot each data point as a point in a d-dimensional space, where d represents the number of features we possess. We can perform classification by finding the hyper-plane that differentiates the two classes best. However, how do we define which hyper-plane is best? let us look at a few different scenarios:
Scenario 1:
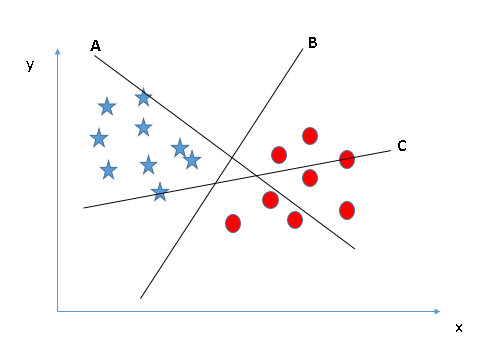
In Scenario 1, there are three hyper-planes: A,B, and C. We want to classify starts from circles, and it is easy to see that B does this best.
Scenario 2:

Here, all three hyper-planes separate the two classes well. But, which one is best? We need to look at maximizing the distance (called the margin) between the nearest data point in either class. We see that the star is closest to B and a little further from C and the closest circle is closest to A. C has a high margin compared to A and B. Thus, we select the hyper-plane C. Selecting a hyper-plane of low margin could give us a high chance of misclassification.
Scenario 3:
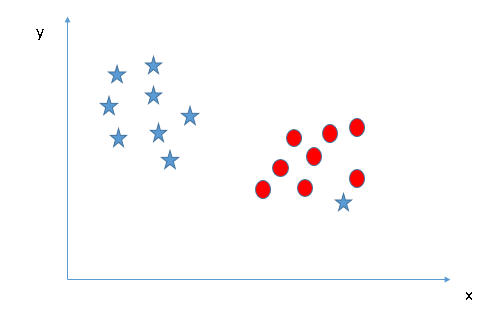
Here we see that there is an outlier. Will SVM be able to separate the classes? Yes, SVM can ignore outliers.
All in all, given a training dataset of n data points $(x_1,y_1),...,(x_n,y_n)$ where the $y_i$ are 1 or -1 indicating the class to which the p-dimensional vector $x_i$ belongs. We want to find the maximum-margin hyperplane that divides the group of points $x_i$ for which $y_i=1$ from the group of points for which $y_i=-1$. This is defined so that the distance between the hyperplane and the nearest point $x_i$ from either group is maximized. We can write any hyper-pane as the set of points $x$ satisfyinh $w \cdot x - b = 0$, where $w$ is the normal vector to the hyper-plane.
Let us now implement the linear SVM classifier in svm_classify.m. We want a function that will train a linear SVM for every category, one v.s. all, and then use the learned classifiers to predict the category of every test image. Every test feature will be evaulated with all 15 SVMs and the most confident SVM will win. We will let confidence, or distance from the margin, be $W \cdot X + B$, where W and B are the learned hyperplane parameters. Our implementation is as follows:
- Parameters:
- train_image_feats is an N x d matrix, where d is the dimensionality of the feature representation.
- train_labels is an N x 1 cell array, where each entry is a string indicating the ground truth category for each training image.
- test_image_feats is an M x d matrix, where d is the dimensionality of the feature representation.
- Return Variable: predicted_categories is an M x 1 cell array, where each entry is a string indicating the predicted category for each test image.
- Setup Variables: We let categories be the unique of the train_labels, num_categories be the length of categories, LAMBDA = 0.0003 (our parameter that controls vm_svmtrain), W and B be empty arrays, and lbl_b be a vector of -1's of size train_labels.
- For Loop: We iterate over the number of categories. We set temp_lbl_b equal to lbl_b. We then create a vector tf that has 0's and 1's where categories(i) is the same as the train_labels. Where they are the same there will be a 1, else there will be a 0. We then set lbl_b(tf)=1. We now transpose train_image_feats and lbl_b and pass them into vl_svmtrain with our lambda and Loss being HINGE2. This will give us Wi and Bi. We then set lbl_b equal to temp_lbl_b and set W(i,:) to Wi and B(i,:) to Bi
- Predicted Categories: We create an empty cell called predicted_categories and then iterate over the size of test_image_feats. We let our confidences be denoted by c and then iterate over the number of categories and add $W \cdot \text{test_image_feats} + B$ to c. We then exit the nested for loop and get the index of max(c). We then add categories(this index) to predicted_categories.
Using LAMBDA = 0.0003 we obtain an accuracy of 63.4% (note that upon running the program there might be slight deviation of a few hundreths but should be very close in accuracy to this number). The charts are as follows:
We note that LAMBDA has strong effects on our accuracy. Let us take a look at accuracys corresponding to a range of lambdas in the table below:
| LAMBDA | Accuracy |
|---|---|
| 0.00001 | 58.87% |
| 0.0001 | 61.73% |
| 0.001 | 62.80% |
| 0.01 | 50.87% |
| 0.1 | 38.80% |
| 1 | 44.47% |
| 10 | 42.27% |
Examining the table above, we can see how important LAMBDA is to vl_svmtrain(). Using a LAMBDA between 0.0001 and 0.0003 gave me higher accuracy, however 0.0003 gave me the highest accuracy of 63.4%.
So Far:
Let us see how we progressed in terms of accuracy so far:
No Implementation
With randomly guessing we achieved an overall accuracy of 6.8%.
Tiny Images & Nearest Neighbors
With normalized tiny features, K=3, and a distance metric of CHI2, we achieved an overall accuracy of 22.8%.
Bag of SIFT representation & Nearest Neighbor
Using a vocab_size = 200, a step_size = 3 in build_vocabulary, and the 'fast' parameter and a step size of 8 in vl_dsift in get_bag_of_sifts we achieved an overall accuracy of 56.4%.
Bag of SIFT representation and linear SVM classifier
With the 'fast' parameter and a step_size=8 in get_bags_of_sifts and a LAMBDA=0.0003 and a Loss='HINGE2' in svm_classify we achieved an overall accuracy of 63.4%.
Graduate Extra Credit:
Vocabulary Size: Previously we used a vocabulay size of 200. We obtained the highest accuracy with the Bag of SIFT representation and linear SVM classifier so let us test the different vocabulary sizes on this pipeline with a LAMBDA=0.0003 and a step size in the build_vocabulary of 3 and the 'fast' parameter.
| vocab_size | charts | Accuracy |
|---|---|---|
| 10 | 43.9% | |
| 20 | 55.5% | |
| 50 | 60.7% | |
| 100 | 63.4% | |
| 200 | 65.1% | |
| 400 | 67.1% | |
| 1000 | 67.6% |
We see that the larger the vocab_size we use the better our results are and the more computational expense we incur, for example with a vocabulary size of 400 it took 5326.331882 seconds. The 0.5 increase in accuracy from 400 to 1000 is not worth the additional computational expense in my opinion. Thus, using a vocab size of between 200 and 400 would be ideal in terms of accuracy and computational expense.
Cross Validation: We can use cross-validation to measure performance rather than the fixed test/train split provided in our starter code. What we want to do is randomly pick 100 training and 100 testing images for each iteration and report the average performance and standard deviations. To implement this we randomly generate 100 numbers (sampling with replacement) and choose these as the indices of our image_paths instead of iterating over all image_paths. We can add our proj4.m code in a loop and run it 10 times and we get the following accuracies: .632, .628, .631, .620, .618, .631, .622, .631, .630, .628. The average of the accuracies is 0.6271. The standard deviation of the accuracies is 0.00515213. We can look at a histogram of these accuracies below:

We see that this is very close to the accuracy we obtained without randomly choosing 100 training and 100 testing images for each iteration.
SUN database: The SUN database at its core has entries that correspond to names of scenes, palces, and environments (any concrete noun which could reasonably complete the phrase I am in a place, or let's go to the place), using WordNet English dictionary. There are 397 scene categories contained in a 37GB file. If we use this data in our data directory and tweak our code for to give us accuracy from the confusion matrix (not plotted since extremly large in length and width) we get an accuracy of 43.2%. It seems that this should be about right for using bag of sift and linear SVM classifier with our settings as in the above section due to the sheer number of categories it contains. Even with extremly finely tuned parameter settings I would see it difficult to reach above 55% accuracy. I omitted the confusion matrix as it is difficult to read as there are 157,609 cells we would need to observe at one time. I believe that with deap learning we would be able to get upwards of 60-70%%. We note that running this dataset is a huge computational expense at every step in our pipeline. This dataset took an enormous amount of time to run on a well equipped machine. The data from this experiment can be downloaded at this link.
We could use the more sophisticated fisher encoding scheme analyzed in the comparative study of Chatfield et al. The fisher vector is an image representation obtained by pooling local image features. Let us describe the process. Let $I = (x_1,x_2,...,x_n)$ be a $D$ dimensional set of SIFT descriptors extracted from an image. Let $\theta = (\mu_k,\Sigma_k,\pi_k: k = 1,...,K)$ be the parameters of a Gaussian Mixture Model fitting the distribution of descriptors. We can get the posterior probability:
$$q_{ik} = \frac{\text{exp}\left(\frac{-1}{2}(x_i-\mu_k)^T\left(\Sigma_k\right)^{-1}(x_i-\mu_k)\right)}{\sum_{t=1}^K \text{exp}\left((x_i-\mu_t)^T\left(\Sigma_k\right)^{-1}(x_i-\mu_t)\right)}$$
If we look at each mode represented by $k$ we can see that the mean vector is:
$$\mu_{jk} = \frac{1}{n\sqrt{\pi_k}}\sum_{i=1}^n q_{ik}\frac{x_{ji}-\mu_{jk}}{\sigma_{jk}}$$
and we see that the covariance vector is:
$$v_{jk} = \frac{1}{n\sqrt{2\pi_k}}\sum_{i=1}^n q_{ik} \left(\left(\frac{x_{ji} - \mu_{jk}}{\sigma_{jk}}\right)^2 - 1 \right)$$
where $j=1,...,D$ spans the vector dimensions. The fisher vector is then $\theta(I) = [...,\mu_k ..., v_k, ...]^T$.
The above derivation looks complicated, but we can make use of the vl package to help us with our implementation.
We create a function called fisher which takes in the train_image_paths and the test_image_paths. It returns the train_image_feats and the test_image_feats. We first iterate over the number of rows in the training paths and use vl_dsift with the single data type image after it has been read in and with the fast parameter and a step size of 5. From this we get sift_feats and we can calculate our features as [features s_sift_feats] where s_sift_feats is a single cast of sift_fets. We then use vl_gmm on features and 30 clusters to get the means, covariances, and priors. We then create two empty arrays: train_image_feats and test_image_feats. We iterate over the number of rows in the train image path and call cl_dsift on both train_sift_feats and test_sift_feat with the fast parameter and a step size of 5. We then use vl_fisher on both of these variables with the means, covariances, and priors. We then transpose these and represent these by the variables enc1 and enc2. train_image_feats then equates to [train_image_feats; enc1] and test_image_feats equates to [test_image_feats; enc2]. We then return these two variabels and can proceed to run linear SVM classification.
We use a step size of 5 because it is fairly dense and runs in a reasonable amount of time. Decreasing the step size will increase the accuracy; however, it will increase the program's run time. After experimenting with different step sizes, I found 5 to be a nice fit between accuracy and computational expense.
Let us now run fisher with linear svm classification with a LAMBDA = .00003 and a step size of 5. We obtain an accuracy of 71.7%. However, if we add the parameter 'normalized' to enc1 and enc2 we get an accuracy of 72.2% The charts are found below: