Project 4 / Scene Recognition with Bag of Words

Building the tiny image representation

I built the tiny images representation to be used as a baseline for comparing with the bags of sift representation. This is not a particularly good representation, because it discards all of the high frequency image content and is not especially invariant to spatial or brightness shifts.

My algorithm is as follows:


num_images = size(image_paths,1);
d = 16;
image_feats = zeros(num_images, d*d);
image_paths(1,1)
for i=1:num_images
    I = image_paths(i,1);
    I = imread(I{1});
    X = imresize(I,[d d]);
    
    %normalizing to zero mean and unit variance  
    % X = X/sum(X(:)); 
    X = X-mean2(X(:));
    X = X/std2(X(:));
    image_feats(i,:) = X(:)';
end

Nearest Neighbour Classifier

I then buiilt the 1-NN classifier that finds the nearest training example for every test case and assigns it the label of that nearest training example. As the dimensionality increases, the classifier cannot learn which dimensions are relevant vs. irrelevant. I achieved relatively higher accuracies using the CHI2 distance metric (vs. the default L2- Euclidean) with a difference of about 3% in accuracy.

My algorithm is as follows:


train = train_image_feats';
test = test_image_feats';
%D = vl_alldist2(train, test);
D = vl_alldist2(train, test, 'CHI2');
[~, min_i ] = min(D);
predicted_categories = train_labels(min_i);

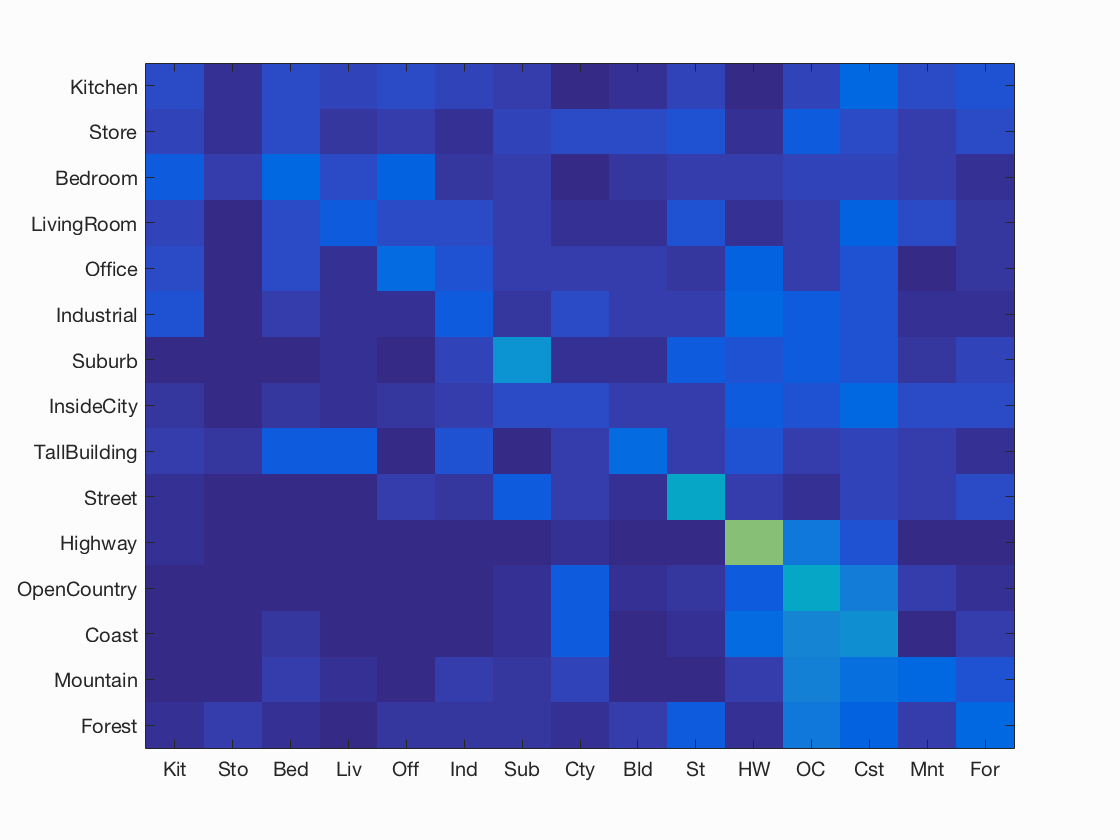
Results of Case 1: Tiny Images + 1NN

I achieved a minimal accuracy of 21.3% Please look at Test 1 for more details. 


Getting paths and labels for all train and test data
Using tiny image representation for images
Elapsed time is 5.235921 seconds.
Using nearest neighbor classifier to predict test set categories
Elapsed time is 2.643928 seconds.
Creating results_webpage/index.html, thumbnails, and confusion matrix
Accuracy (mean of diagonal of confusion matrix) is 0.213

Building the vocabulary of visual words

I did this by sampling about 900,000 sift features from the training set and then clustering them with kmeans. For each image I randomly picked 600 features (thus 600*1500 = 900,000) The centroids are the visual word vocabulary. I tried with 2 values of k: 50 and 200(performance reported below). Since this was taking about 20 minutes with vl_dsift and step size of 3, I used the 'fast' parameter and step size of 5, for faster run time.

My algorithm is as follows:


num_features = 600;
N = size(image_paths, 1); 
combined_features = [];
for i = 1:N
    I = image_paths(i,:); 
    image = imread(I{1}); 
    image = im2single(image);
    [~, SIFT_features] = vl_dsift(image,'step',5,'fast'); 
    %size(SIFT_features)
    
    %pick num_features randomly
    perm = randperm(size(SIFT_features,2));
    rand_i = perm(1:num_features);
    SIFT_features = SIFT_features(:, rand_i );
    
    %add them to a big set of features.
   combined_features = horzcat(combined_features,SIFT_features);
end
[centers, ~] = vl_kmeans(im2single(combined_features), vocab_size); 
vocab = centers';

Bags of SIFT representation

Now for every image, I counted how many SIFT descriptors fall into each cluster in our visual word vocabulary (nearest neighbor centroid) and built a histogram. Also normalized it so that image size does not dramatically change the bag of feature magnitude.

My algorithm is as follows:


load('vocab.mat')
nbins = size(vocab,1);
N = size(image_paths,1);
image_feats = zeros(N,nbins);
tic
for i = 1:N
    I = image_paths(i,:); 
    image = imread(I{1}); 
    image = im2single(image);
    [~, SIFT_features] = vl_dsift(image,'step',5,'fast'); 
   
    D = vl_alldist2(vocab',im2single(SIFT_features));
    [~ , min_i] = min(D);
    num_features = size(min_i,2);
    sift_rep = (hist(min_i, nbins))/num_features;
    image_feats(i, :) = sift_rep; 
end

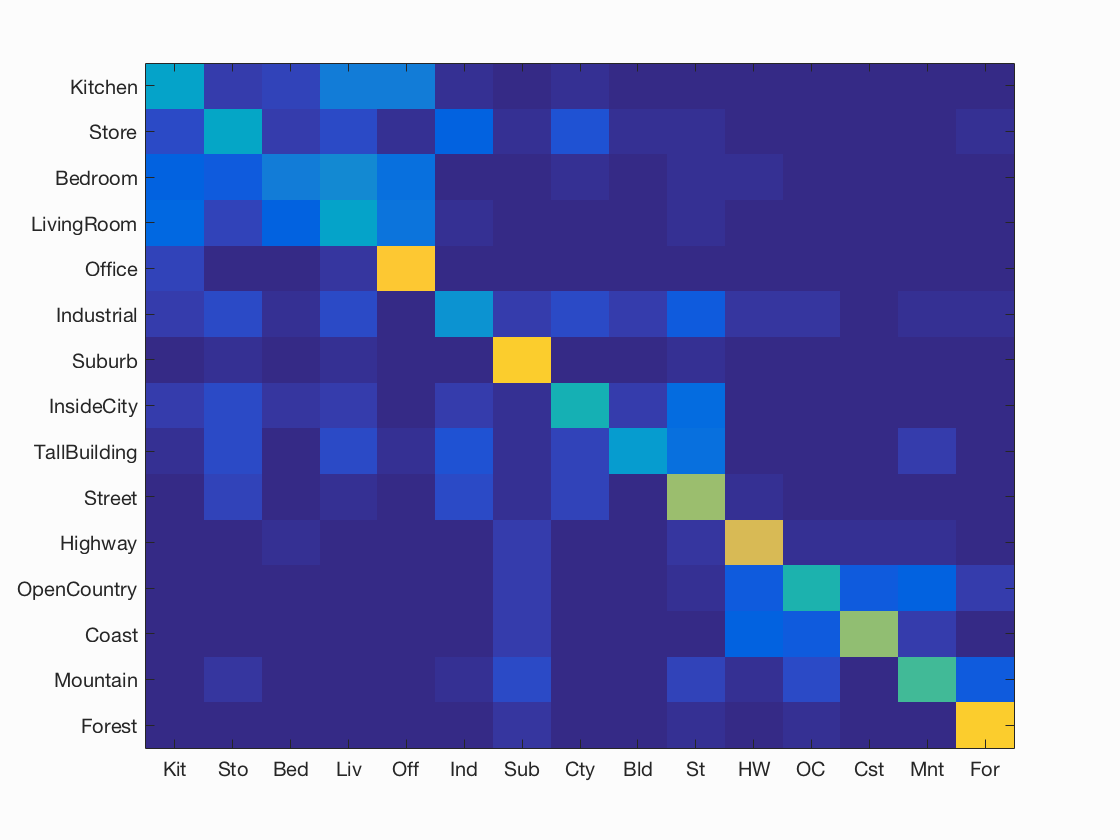
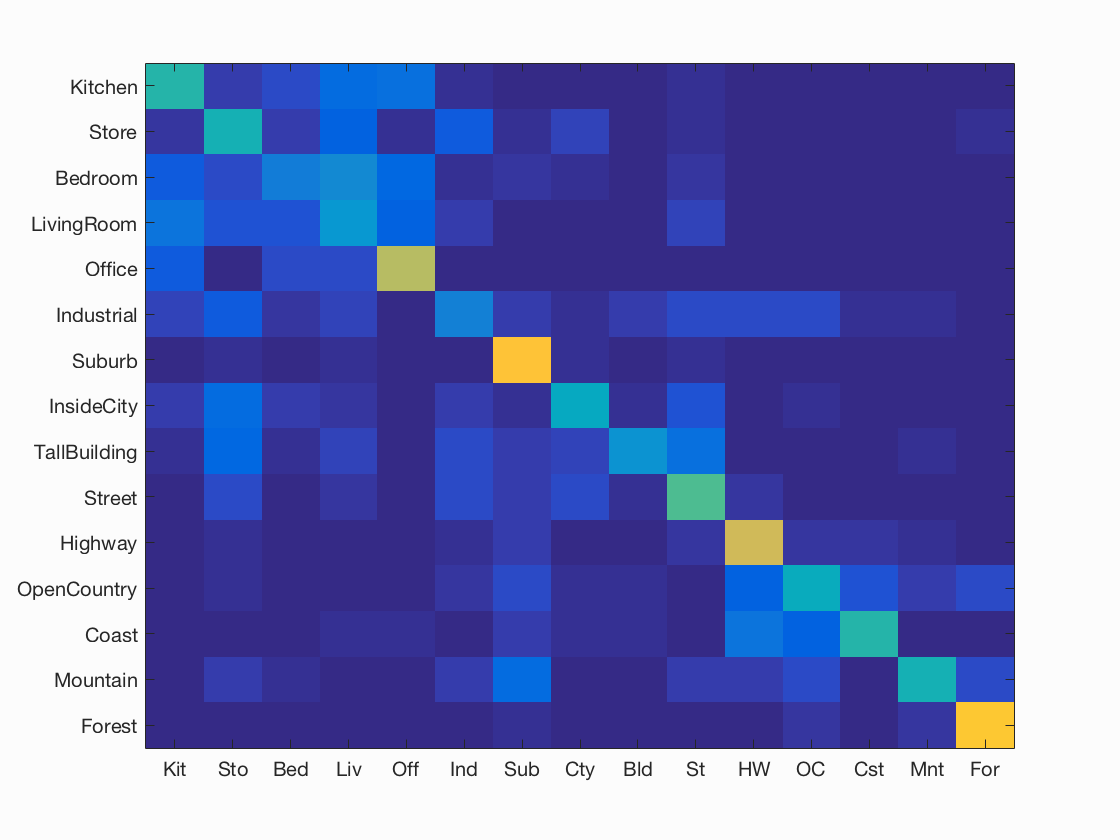
Results of Case 2: Bags of SIFT + 1NN

I achieved an accuracy of 54.1% for K=200 and 49.7% for k=50. Please look at Test 2 (k=200) and Test 2 (k=50)for more details.

K= 200, Accuracy = 54.1% K = 50, Accuracy = 49.7% 

Getting paths and labels for all train and test data
Using bag of sift representation for images
building vocab
Elapsed time is 126.566850 seconds.
getting sift bag
Elapsed time is 99.041953 seconds.
Elapsed time is 99.596549 seconds.
Using nearest neighbor classifier to predict test set categories
Elapsed time is 2.149116 seconds.
Creating results_webpage/index.html, thumbnails, and confusion matrix
Accuracy (mean of diagonal of confusion matrix) is 0.541

1 vs all Linear SVM

I trained 15 binary, 1-vs-all SVMs. 1-vs-all means that each classifier will be trained to recognize 'forest' vs 'non-forest', 'kitchen' vs 'non-kitchen' etc. All 15 classifiers will be evaluated on each test case and the classifier which is most confidently positive "wins". For lambda I tried several values like 0.1, 0.001 and ultimately went ahead with 0.000001 (highest observed accuracy). For this again, I've reported values for K=50, 200 below.

My algorithm is as follows:


categories = unique(train_labels); 
num_categories = length(categories);
LAMBDA = 0.000001; 
test_score = [];
for i = 1:num_categories
    labels = strcmp(categories(i), train_labels); 
    labels = +labels;
    ind = find(labels==0);
    labels(ind) = -1;
    [W ,B] = vl_svmtrain(train_image_feats', labels, LAMBDA); 
    test_score = [test_score; W'*test_image_feats' + B];
    
end
[~ , ind] = max(test_score);
predicted_categories = categories(ind');

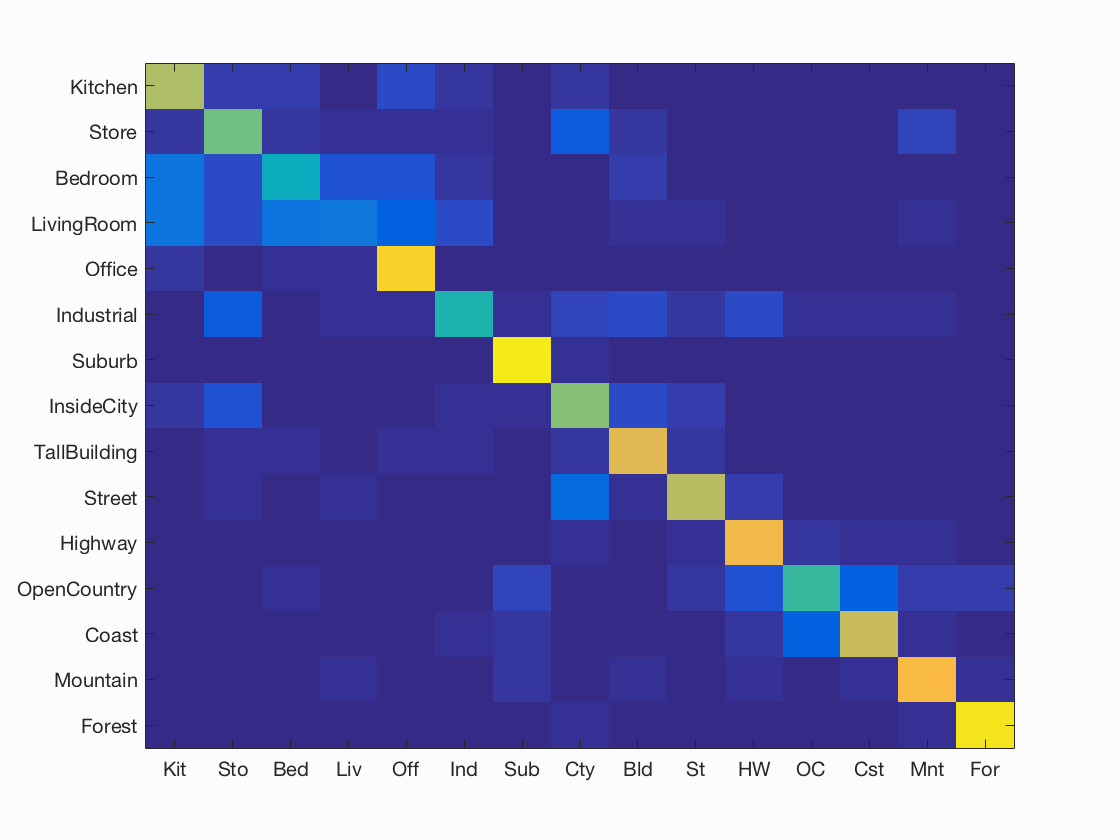
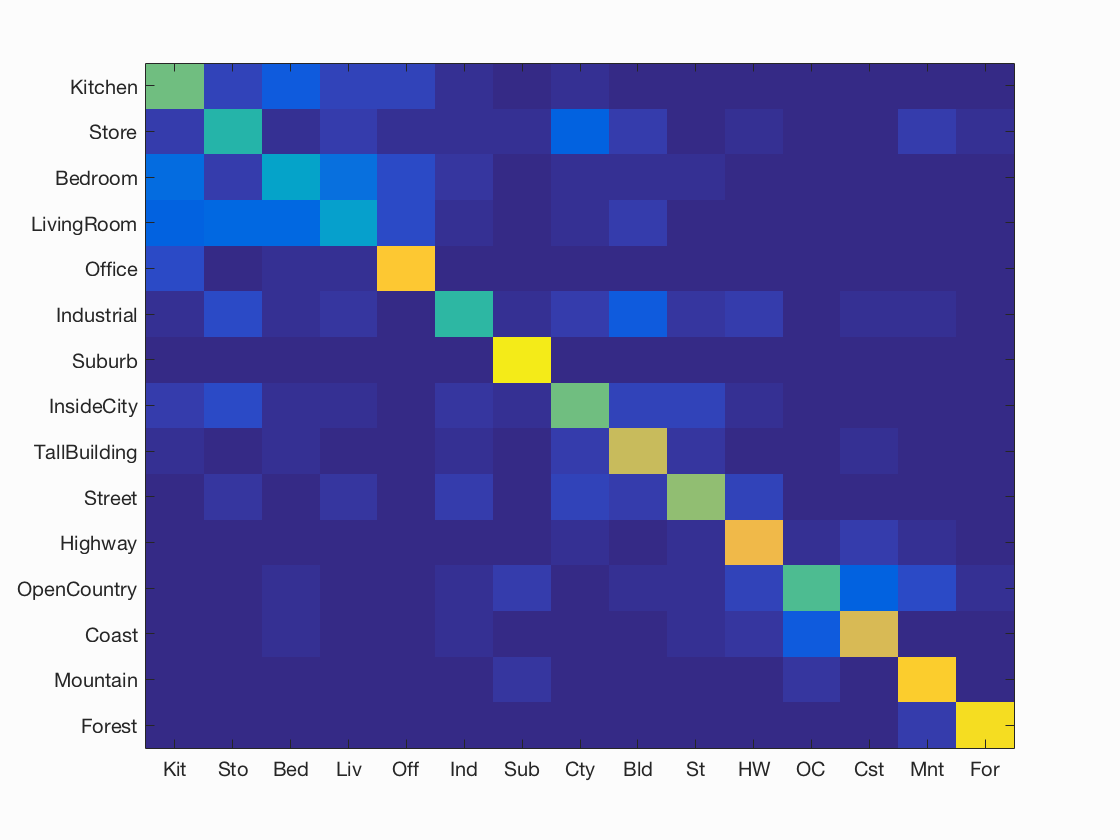
Results of Case 3: Bags of SIFT + Linear SVM

I achieved an accuracy of 67.3% for K=200 and 66.3% for k=50. Please look at Test 3 (k=200) and Test 3 (k=50)for more details.

K= 200, Accuracy = 67.3% K = 50, Accuracy = 66.3% 

Getting paths and labels for all train and test data
Using bag of sift representation for images
No existing visual word vocabulary found. Computing one from training images
Elapsed time is 114.909931 seconds.
getting sift bag
Elapsed time is 102.436123 seconds.
Elapsed time is 103.10002 seconds.
done sift bag
Using support vector machine classifier to predict test set categories
Elapsed time is 7.491537 seconds.
Creating results_webpage/index.html, thumbnails, and confusion matrix
Accuracy (mean of diagonal of confusion matrix) is 0.673

Extra Credit Section

Attempted the following with results shown below:

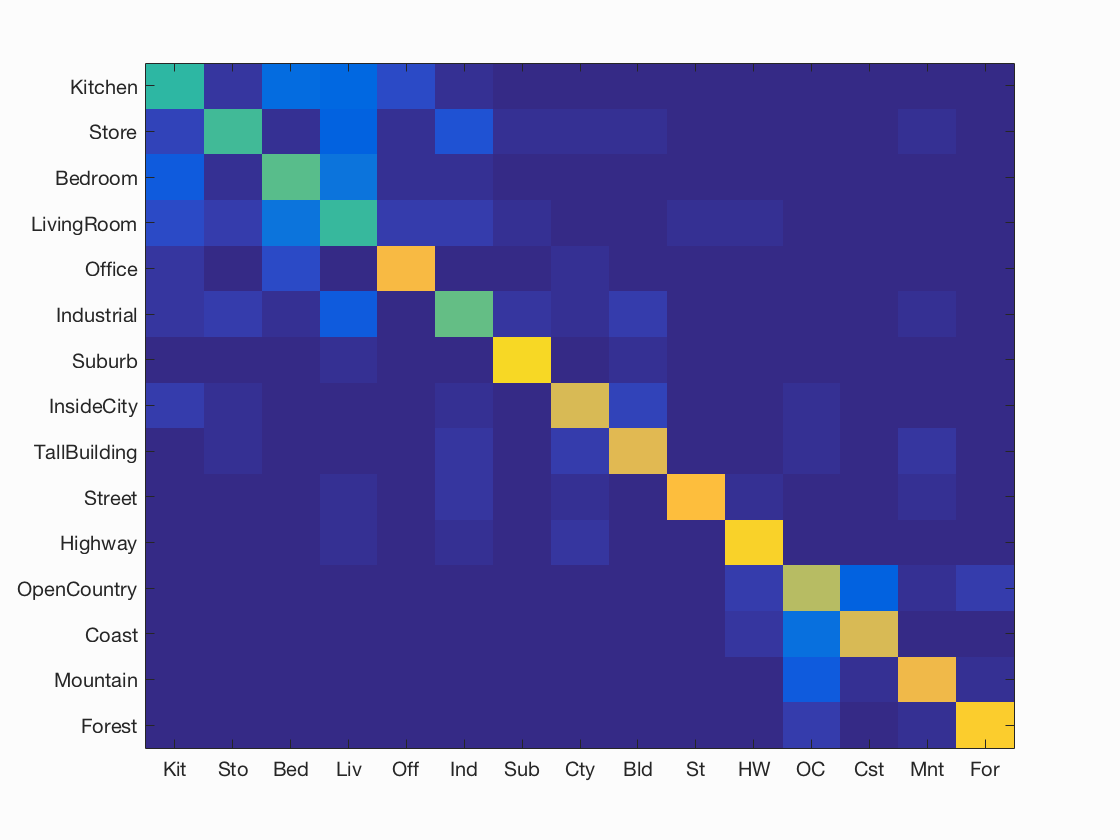
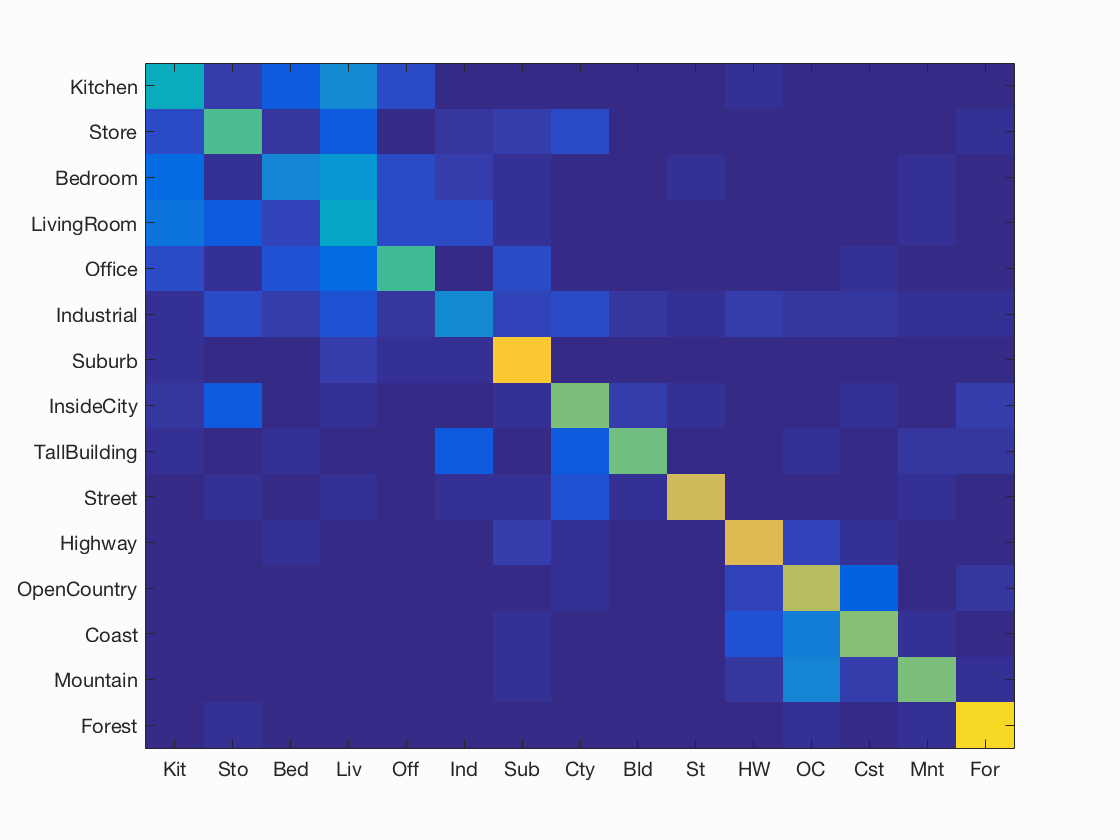
Results using GIST and soft assignments for histograms (K=200):

I achieved an accuracy of 72% for SVM and only 58.5% for Nearest Neighbour. Please look at GIST and SVM and GIST and NN for more details.

SVM, K= 200, Accuracy = 72% 1-NN, K = 200, Accuracy = 58.5%

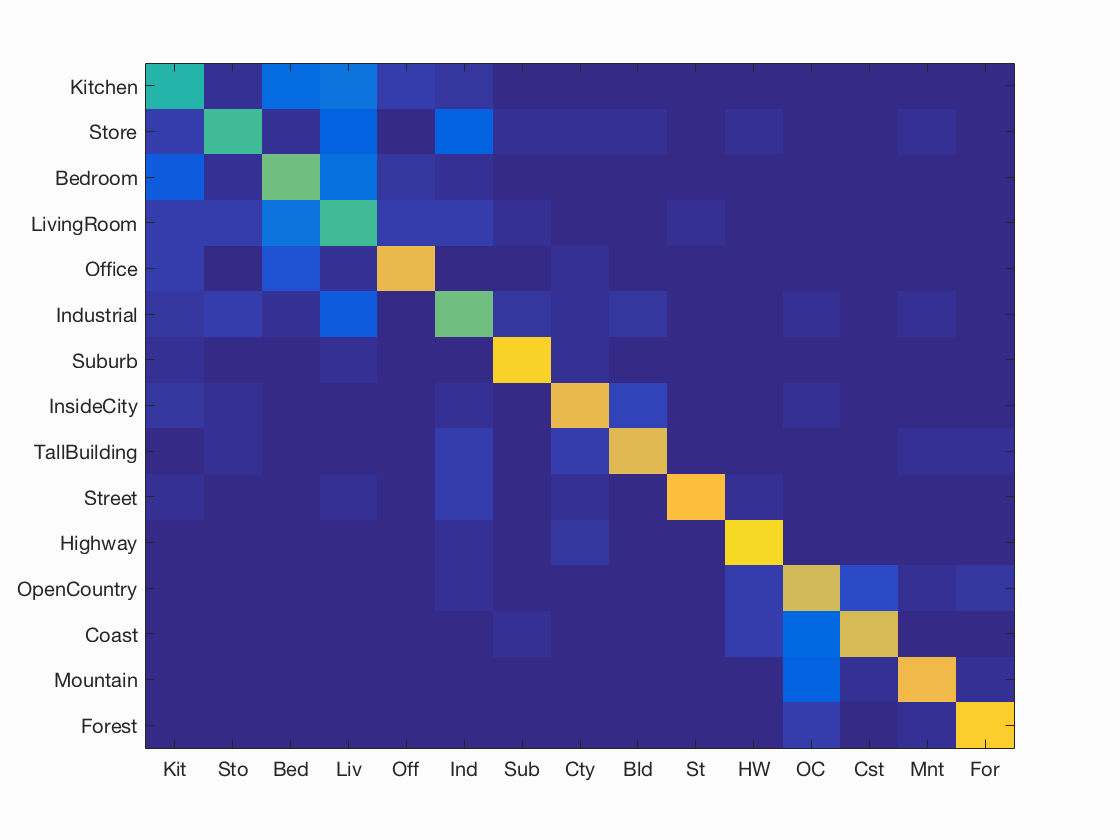
Results using spatial pyramid, SVM (K=200):

I achieved an accuracy of 72.6%. Please look at Spatial Pyramid for more details.

SVM, K= 200, Accuracy = 72.6%

THANK YOU!