In this paper, we explore the learning that occurred in two types of collaborative learning environments in a seventh grade life sciences classroom: an intra-group environment and an intergroup environment. Students used both types of collaboration tools, each tuned to the needs of the task they were doing within or across groups.

We found that the learning outcomes in the two collaborative settings were different. During the intra-group collaboration, students focused more on the structure and behavior of the designs. The inter-group environment on the other hand, led them to discuss the function/s of their models, ask for and provide justifications for the functions. We discuss the results and suggest integration of the inter and intra group tools.

Keywords– classroom discourse processes, K-12 collaborative learning strategies,tools to support teaching in collaborative settings

Outcomes of computer supported collaborative learning are influenced by several factors. Some of these are the composition of the pairs or groups (Whitelock, Taylor, O’Shea, Scanlon, Clark, & O’Malley, 1993), the nature of the task (Puntambekar, 1996) and the nature of the environment itself (Crook, 1994). These factors, either singly or in combination, lead to different interactions among the learners; the types of interactions heavily influence the learning outcomes. In addition, learning outcomes in a CSCL environment are also influenced by the instructional roles that the tools support and when the tools are used in the learning process (Koschmann, 1996).

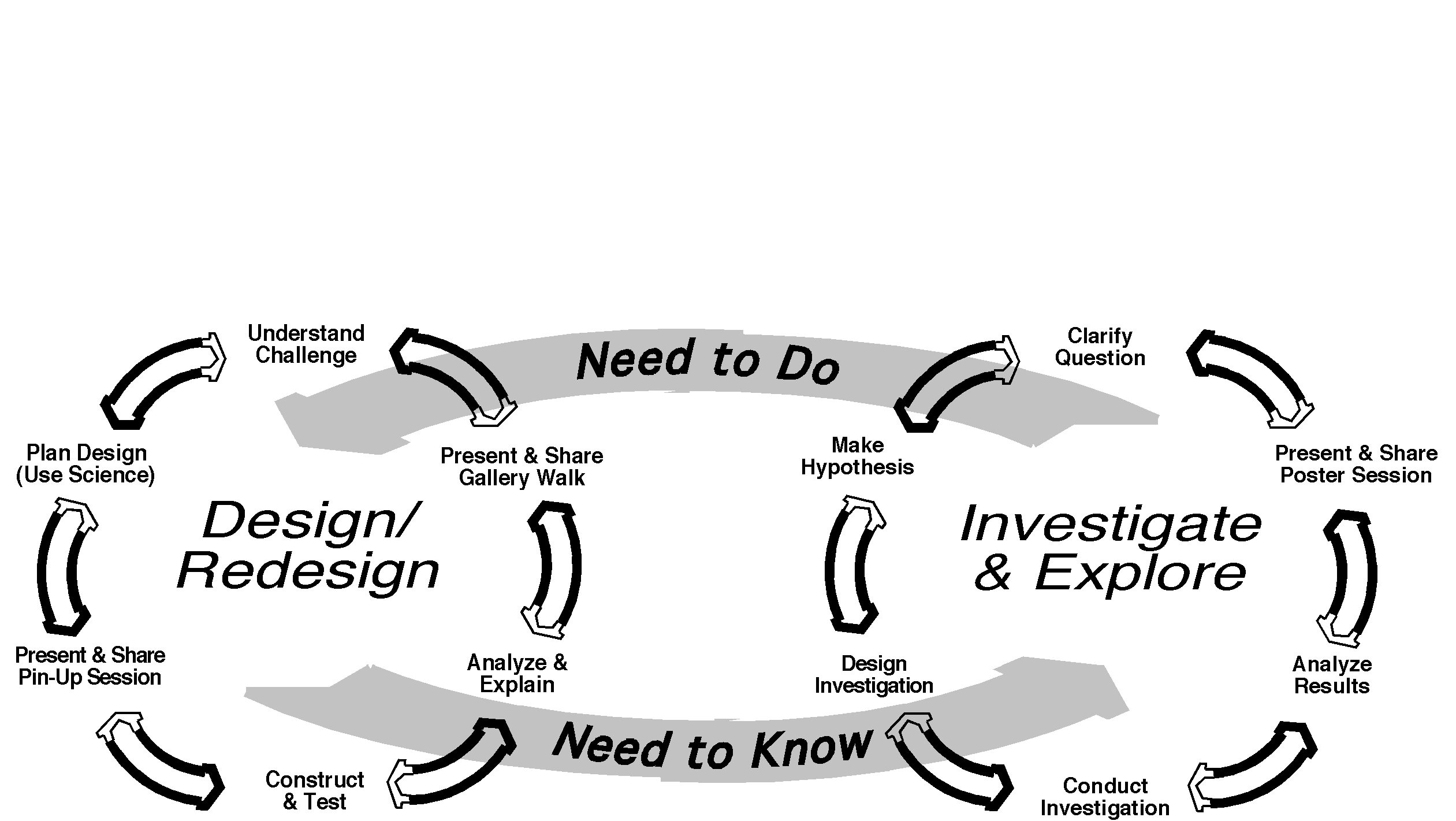
In this paper, we explore the learning that occurred in two types of collaborative learning environments in a seventh grade life sciences classroom: an intra-group environment in which the collaboration was synchronous, scaffolded, without computers and within the groups (the group journals), and an intergroup environment in which the collaboration was asynchronous, with much less scaffolding, with a computer tool (Web-SMILE), used between the groups. Students used both an intergroup collaboration tool and an intra group collaboration tool, each tuned to the needs of the task they were doing within or across groups. We analyzed the student discourse using the the SBF model (based on a model by Goel, Garza, Grue, Murdock & Recker, 1996) that explains design of physical devices in terms of the Structure (the component parts), Function (the functions of the parts) and Behavior (which refers to the causal relationships between the functions of the various components of the system resulting in an action). We found that the learning outcomes in the two collaborative settings were different. During the intra-group collboration students focused more on the structure and behavior of the designs. The inter-group environment on the other hand, led them to discuss the functions of their models; ask for and also provide justifications for the functions. We discuss these results and suggest integration of the inter and intra group tools.

The study was part of the Learning by Design project, aimed at helping middle school students learn science by having them engage in design problems. Learning by Design (LBD) is being developed at Georgia Tech's EduTech Institute as an approach to teaching science, integrated with math and technology, in middle schools. Based on Problem-Based Learning (Barrows, 1985), our conception of LBD (Kolodner, 1997) is that a design problem is posed to children, who then collaborate, with the teacher acting as a facilitator, to propose solutions, decide what they need to learn to follow through or decide between proposed alternatives, seek out that knowledge, and incrementally construct, evaluate, analyze results, and revise ideas and designs. Based on our initial understanding of the complexities of learning from design activities, we have provided students with tools that help them collaborate and also tools that scaffold the design process.

In this particular study, students were asked to design a robot with arthropod features that will ‘live’ on an island and collect information for scientists. The teacher wanted her students to concentrate on the types of locomotion in the arthropods and she specifically constrained the problem to focus students’ designs on the way the arthropods moved. Students in three life sciences classrooms from a suburban public school participated in this project. Students worked in groups of four. There were seven groups in each class, a total of twenty one groups. The project lasted for three weeks in which students conducted research, decided which arthropod they would use as a model for their robot, built quick prototypes and presented their designs to the class.

To help students with the design process, we provided them with 'group journals' that helped them collate their ideas and come to a consensus during four important phases of the design process viz. generating learning issues, writing a specification, choosing a solution, and redesigning their models. In addition they also wrote the philosophy or purpose of their models. This comprised the intragroup part of the collaboration.

After each group had reached a consensus on a design idea, they shared these ideas with other groups, using the computer supported collaborative tool, Web-SMILE. The teacher directed the groups to review the solution ideas of another group. This comprised the inter-group collaboration portion of the learning process.

The group journals were designed as a vehicle for providing hints to students as they were engaging in design activities. Students had their pages open in front of them as they were deliberating. They also aimed to help students reflect on and articulate their design related activities. The journals provided them with guidelines to enable them to make decisions and articulate their ideas during important stages in their learning by design experience as described below.

Design problems are complex and often lead to situations where the student realizes that in order to progress, new information has to be acquired. Borrowed from the Problem-based learning philosophy, generating learning issues is an important aspect of the LBD curriculum. Students are encouraged to generate learning issues in order to know more about the design problem they are working on. This process needs to be orchestrated very carefully to help students to identify what they need to learn. They don't start out with the knowledge they need to identify what they need to know. The journals contained prompts that helped students to think about what they already know and what they needed to know in order to proceed with their designs. Students used the prompts (in the journals) and made a list of the issues they wanted to research in their group journals.

A specification is a detailed description of the problem to be solved. It should spell out exactly what the design must achieve, taking into account the constraints which will affect the solution. A specification should only describe what is required, it must outline specific details of the design that are to be satisfied. The journals helped students to come to a consensus regarding what function their robots will achieve and how the structure of the robot will affect the function / functions.

This is a very complex stage, in which multiple possibilities are generated for each piece of the problem, multiple ways of configuring them to get to a final result of the whole problem are attempted, prediction of the outcomes of each are attempted, and out of the many generated alternative solutions, one is chosen for follow-on activity. This process was orchestrated by in the following way. Students each came up with one solution individually. They rated the positive and negative features of this solution on their own. They then discussed the best solution for the group based on input from all members of the group. The group journals provided the students with a matrix in which they could compare the solutions with respect to the criteria that were satisfied by each (see figures 1 and 2). They rated their solutions along each of the criteria and chose the one that best satisfied the specification of the problem.

Figure 1: ‘Choosing a Solution’ page from the group diary, where students weighed their choices against criteria

Figure 2: Zoom in view of the same page showing the criteria and student evaluation scheme

As a final part of the project, the group journal allowed students to summarize their experiences and specifically prompted them to think about how their designs satisfied the required functions, whether they needed to redesign and how they would redesign.

Figure 3. An example from a group journal

Students were asked to justify their choice of the arthropod that they wanted to model based on the features and how the features would lend themselves to be the best for the environment chosen (see figure 3). This aspect was initiated by the teacher and students had to justify their choice of arthropods both in writing and in oral presentations.

Web-SMILE was developed at the EduTech Institute as a resource for the learning-by-design curriculum. Web-SMILE integrates synchronous and asynchronous collaboration. It is implemented using the World Wide Web and can be accessed from anywhere with a WWW browser. It has electronic whiteboards which provide shared space for record keeping and reflecting. Web-SMILE also provides for collaboration through an asynchronous, threaded discussion area directly evolved from WebCamile (Guzdial & Turns, 1997). Students using Web-SMILE post material to the network that they want others to see, carrying on threaded discussions on topics of their choosing (see figure 4). Procedural facilitation provides typing for the notes and suggested starter text for each type. Students can either post new ideas, create a follow-up to an idea posted earlier, or post a response to an idea from another group.

Figure 4. Web-SMILE Class Discussion area.

Web-SMILE is very easily operated by middle school students. It is relatively fast and very reliable when served on an intranet of eight PowerBook computers within the classroom. Students are able to maneuver through the software environment, with minimal instruction. Students grasp the internet browser interface of this web-based software very quickly and are able to share ideas and respond asynchronously via the network.

During the project described in this paper, the discussion area was used by all twenty-one groups in the three classes (N=84) to share ideas across groups and classes and to peer review alternative solutions considered. They had already weighed the alternatives in their own groups. They used the discussion area to consider the solutions of other groups and give feedback. The teacher instructed them to post the solution idea of their own group and then to respond to other groups.

All students in the groups first used the group journals, and then the same groups used Web-SMILE on the computers. Students used the group journals all through the design process and had them in front of them while making design decisions. They discussed issues relating to their design such as generating learning goals, choosing a solution, etc. and jotted down their decisions in the journals. The software was used by the students specifically to inform other groups of their ideas, provide feedback to other groups and reflect on the solutions before they started to build their models. Both the journals and the software were used for approximately three hours each, by each of the groups. The collaboration provided by the software environment was thus a continuation of the discussions that students had had in their own group.

Sixteen group journals were analyzed for evidence of SBF in terms of the breadth of the notes and the representational issues. The class discussion area notes contributed by these same sixteen groups were also analyzed. The dimensions along which we analyzed the data are described below.

The SBF-model is a framework in which a design can be described. SBF stands for Structure, Behavior, and Function. Structure refers to the parts or components of an artifact or device. This includes the parts shape, color, material, etc. Responses such as "our design, the all-terrain Beetle has two desert legs and two climbing legs" were in this category. Behavior refers to the causal relationships between the functions of the various components of the system resulting in an action. An example for behavior "Adhesive legs are good idea. .. so they can climb flat or rough vertical things" or "Bees can fly forward, backward, sideways and hover in a plane". Function describes what the design is supposed to achieve. Function can be described at the level of the individual components (function of the parts) and at the level of the whole device or artifact itself. For example " the climbing legs are used for going up tall mountains and steep cliffs" is a response that falls into this category.

The context can be defined as the relationship of design to the specified environment. The context was very important in this project because the students had to justify their choice of the arthropod in terms of its adaptability to a specific terrain.

Justification took two forms. Students either justified their design in terms of why they were appropriate for the specific environment because of its features or they asked other groups to justify their choice. For example "How are you going to make your model fly?" was one such question that students asked another group. A more detailed example is "You have a good idea. How are you going to make your model fly ? One idea that we had was to put a small motor inside of the model. It would have wings like an airplane. Another question that we had was if it was durable. If it is durable we are sure that your model will be very successful."

This category included design concerns, such as durability and cost. We call it 'general' because the students were only building models and cost and durability were not significant in that context.

Figure 5. An illustration of the note entry display.

Entries in the group journals and notes from the discussion area were coded by two raters for evidence of the above mentioned categories. The student entries in each collaborative tool were analyzed for multiple responses in each of these categories. The responses in each category are expressed as a ratio of the total number of responses in Table 1. Students' responses were examined in the two conditions of collaboration.

Students' responses in each of the categories were compared for the two conditions of collaboration. The two types of collaborative environments led to completely different outcomes. Students' responses reflected that the issues they addressed were not the same in the two conditions; the difference in the emphasis placed on certain issues and not others under each condition was the most important finding of this study. The two collaboration scenarios complemented each other, together they covered the range of issues we wanted the students to be thinking about.

We found that the number of responses in the structure category were significantly more in the intra-group (t=6.03; p<.001) than in the intergroup condition. Students closely considered the component parts of the arthropods they were designing. Closely related to the issue of the structure was the fact that students' responses reflected that they recognized the significance of behavior as an important aspect of their robots, especially because it had to function in a specified environment. The journal entries for the behavior category (t=7.22; p<.001) and the environment category (4.95; p<.01) were significantly more than the ones for the same categories in the Web-SMILE notes.

Table 1. The number of responses (ratios) in each category

From observations, other than statistical analysis the journals entries were also richer in the breadth of the issues addressed. Students discussed criteria such as balance, actuation and control of their robots which were concepts that they had been introduced to by a robotics expert.

The issues that students addressed while they were working in the computer supported environment were not the same as in the design journals. While students had more responses in the structure, behavior and environment categories in their journals, their notes from Web-SMILE showed that they were more concerned with the functioning of the parts of their arthropod-robots. They were also posing questions to their peers and asking for justifications. The number of responses for the function category was significantly more (t=5.46; p<.001). The justifications category included responses that were requested and justifications that were provided by the groups. Responses in this category were significantly greater when students used the computer tool (t=4.64;p<.001). Another category that students had a greater number of entries was the 'general' category, which included aspects such as durability and cost. Some notes were very short and cryptic while some were in greater detail. Figure 5 illustrates the note entry display. The type of note is selected from a pull-down menu, then there are several suggestions for text lead-in to procedurally facilitate the student with the note content. The displayed note is the actual note entered as a response to a design based on three arthropods. This group analyzed the proposed design at all three levels. They saw functions of locomotion and protection; behavior of restricted motion; and structural components included body shell, legs and wings.

Results indicate that the two kinds of learning tools used in the two collaborative learning situations fostered different levels of knowledge aquisition. The group design journals, representing the synchronous scaffolded collaboration without computers, portrayed a deeper level of analysis based on the predominance of behavioral, structural and environmental responses showing a more significant level of domain knowledge. In this collaborative setting, the students actually articulated adaptation as an important aspect of the study of arthropods. Students reasoned about how arthropods are different in terms of their structure and behaviour, and how these features help them adapt to their environments.

The software discussion area, representing the asynchronous, virtually unscaffolded collaboration with computers, showed more evidence of justification, both requesting and providing a basis to the specified design. However, the level of analysis was not as often concerned with components and behavior, as with a higher level of functionality. There were many more notes designated as simply general discourse, not dealing with any aspect of design. The students tended to follow one thread of discussion, rather than to review several ideas from several groups. Consequently, the longer threads were no more productive than the shorter ones.

The two conditions complemented one another, not only because of the nature of the tools but also because of when they were used within the design process and also the instructional purpose reinforced by the teacher. The group journals were developed to be used in all phases of the design process. They included prompts that helped keep the students focused on the task. Students used them to discuss significant issues during the design process. The teacher made it clear that the final objective of their journals would be to advise a scientist to build a specific robot. Thus their entries were more often at the structural and behavioural level required to adequately describe a design.

On the other hand the discussion area was developed to share ideas and request feedback which is appropriate in some phases of the design process. This tool provided a forum for more divergent discussions. The teacher directed the use as a peer review tool. Consequently the duscussion notes remained at a more conversational level. This did elicit request for justification which is important for knowledge building.

In this study we found that no one set of activities and scaffolding was sufficient for eliciting the full range of consideration of issues in students; the within-group design work (scaffolded by the group journals) pushed students to focus on structure and behavior while the between-group critical analysis and sharing work pushed students to consider functions and how to achieve them. Since both are important for learning, collaboration tools and collaboration activities should be designed to ask students to do the full range of reasoning they need to do. We supported generation of ideas with our within-group tool and using between-group collaboration to focus criticism and discussion about the ideas. In future generations of the work, we will aim to computerize and integrate the two collaboration tools and to design a better between-group environment that explicitly supports sharing of design ideas and critique and analysis.

Barrows, H. S. (1985). How to design a problem based curriculum for the preclinical years. Springer-Verlag: NY.

Crook, C. (1994). Computers and the Collaborative Experience of Learning. London, England: Routledge.

Goel, A., Garza, G., Grue, N., Murdock, W. & Recker, M. (1996). Exploratory interface in interactive design environments. In J. S. Gero & F. Sudweeks (eds.), Artificial intelligence in design, 387-405.

Guzdial, M., & Turns, J. (1997). Technological Support for Anchored Collaboration : Draft.

Kolodner, Janet L. (1997). Educational Implications of Analogy: A View from Case-Based Reasoning. American Psychologist.

Koshmann, T. (1996). Paradigm Shifts and Instructional Technology: An Introduction. In T. Koshmann (Ed.), CSCL: Theory and Practice of an Emerging Paradigm (pp. 1-24). Mahwah, New Jersey: Lawrence Erlbaum Associates.

Puntambekar, S. (1996) Investigating the effect of a computer tool on students' metacognitive processes. Unpublished doctoral dissertation, School of Cognitive and computing sciences, University of Sussex, UK.

Whitelock, D., Taylor, J., O’Shea, T., Scanlon, E., Clark, P., & O’Malley, C. (1993). What do you say after you have said hello? Dialogue analysis of conflict and cooperation in a computer supported collaborative learning environment. Paper presented at the 11th international PEG conference, 2nd - 4th July 1993, Edinburgh.

Sadhana Puntambekar, Kris Nagel, Roland Hübscher, Mark Guzdial and Janet L. Kolodner: Edutech Institute, Georgia Institute of Technology, GCATT Building, 250 14th Street, N.W. Suite #138, Atlanta, GA 30318-0490. sadhana@cc.gatech.edu, kris@cc.gatech.edu , roland@cc.gatech.edu, guzdial@cc.gatech.edu, jlk@cc.gatech.edu.