

 |
AN INTRODUCTION TO
NEWTONIAN MECHANICS by Edward Kluk Dickinson State University, Dickinson ND |
MECHANICAL ENERGY
Introduction
A concept of kinetic
and potential energies in mechanics emerges from Newton second
law. It is hidden there and to reveal it we need a little bit of
mathematics. For sake of simplicity let us consider an object
with mass m moving along vertical
x - axis under influence of constant
gravitational force mg. If the x
- axis is directed up then Newton second law for this
object can be written as follows
m Dv/Dt = - mg .
Multiplying both sides of it by velocity v which is defined as Dx/Dt we obtain
m v Dv/Dt = - mg Dx/Dt .
But v Dv can be replaced by D(v2/2) . The proof of this last statement is not very complicated. By its definition (see the former page about Newton second law)
D(v2/2) = v2(t)/2 - v2(t - Dt)/2 = 1/2 {v2(t) - v2(t - Dt)} = 1/2 {v(t) + v(t - Dt)}{v(t) - v(t - Dt)}.
The last result is obtained with help of well known algebraic identity a2 - b2 = (a + b)(a - b). In the first figure bracket in this result v(t - Dt) can be replaced by v(t) with no practical change to the value of this bracket. For better understanding of it let us assume that v(t) = 3.001 and v(t-Dt) = 3.000. Thus the exact value of the bracket is 6.001, whereas its approximate value after v(t - Dt) is replaced by v(t) would be 6.000. The ratio of these two results is very close to one so they are almost identical. Notice that it does not make a sense to apply the same approximation to the second square bracket because its exact value would be 0.001 and its approximate value would be 0. The ratio of these two numbers (if 0.001 comes first) is an infinity so these numbers are very different. As a matter of fact we do not need to apply any approximations to the second bracket because it is equal by definition to Dv. All of it let us replace the second equation from the top by
D(mv2/2)Dt = - D(mgx)/Dt or D(mv2/2 + mgx)/Dt = 0 .
The last result means that the quantity mv2/2 + mgx for the discussed body does not change during its motion. Using the physics language (or jargon if you prefer) we say that this quantity is conserved. This relation between v2 and x was experimentally discovered by Wilhelm Leibniz (1646 - 1716) in the end of seventeen century who had laid the ground for idea of energy and idea of conservation laws (for more information about this subject you may read "Energy Is Not The Ability To Do Work" by Robert L. Lehrman published in The Physics Teacher, 15, 15, (1973)). The word energy for the quantity mv2/2 + mgx was proposed by Johann Bernoulli (1667-1748) in 1717. Later the first term of this quantity, mv2/2, was named a kinetic energy, and the second term, mgx , was named a potential energy. Now the sum of both terms we call a mechanical energy and its constancy during the motion a mechanical energy conservation principle (law). Notice that both Leibnitz and Bernoulli were the great mathematicians. This fact shows again importance of mathematics for physics.
Units
Three fundamental SI units in mechanics are kilogram (kg) for mass, meter (m) for length and second (s) for time. All other units in mechanics are derived from definitions of relevant magnitudes or fundamental relations in which these magnitudes appear. Looking at the mathematical formulation of Newton second law ma = F we see that the basic unit of force must be a product of basic unit of mass and basic unit of acceleration. It results with kg m / s2 which is called Newton (N). Similarly for momentum its definition p = mv leads to the unit kg m / s . This unit does not have any special name or symbol. The basic unit of energy can be derived from the definition of kinetic energy K = mv2/2 or potential energy U = mgh. In both cases we end up (as we should) with kg m2 / s2 . This unit is called Joule (J) after English physicist James Prescott Joule. Notice that deriving units we apply to them the same algebra rules like for other magnitudes.
Experimental verification of mechanical energy conservation principle
In the former experiment verifying Newton second law you have collected data which can be used for verification of mechanical energy conservation for the investigated system. In this experiment you have measured elapsed times t as the block covered distances x = 2 m, 4 m, 6 m, 8 m and height of the hanger was declining to h = 6 m, 4 m, 2 m, 0 m. The velocities of the block at each of these distances can be calculated from the relation v = at , where a is the already calculated block acceleration. As the block accelerates its kinetic energy increases, so does kinetic energy of the hanger. Because their speeds are identical their total kinetic energy K = (mB + mH) v2/2 . Potential energy of the block does not change because the block moves on the horizontal plane, but potential energy of the hanger mHgh declines because the hanger is falling down. Then the total potential energy of the system U = mHgh , and the total mechanical energy of the system E = K + U.
Now select one set of your "experimental" results for a fixed mass of the hanger, than copy and fill the following table calculating velocities and all involved energies with help of formulae which were discussed above.
| x (m) | h (m) | t (s) | v (m/s) | K (J) | U (J) | E (J) |
0 |
8 |
0 |
0 |
|||
2 |
6 |
|||||
4 |
4 |
|||||
6 |
2 |
|||||
8 |
0 |
Study your final results and find out if the mechanical energy of the system is conserved. Notice that in our "experimental" procedure we have avoided necessity of velocity measurements. This avoidance was possible only because we know for this case how velocity depends on time.
Beside gravitational potential energy there are many other types of potential energies. One of them is elastic potential energy which can be stored in springs. If a coil spring is compressed or stretched, it is able to push or pull an attached object delivering to this object kinetic energy. The kinetic energy appears there as the result of conversion of spring elastic potential energy. This conversion take place as the elastic force Fe produced by the spring accelerates the object.
For a quantitative discussion of this case we have to know how Fe depends on the spring elongation x . The simplest way to find it out is to suspend the spring vertically and hang on it several different masses m . Each of these masses is pulled down by the gravity force Fg = mg and this force is stretching the spring. If the mass stays at rest , Fg is equilibrated by Fe of the same magnitude, but opposite direction ,making a net force acting on the mass equal to zero. Measuring the elongation x and graphing Fe versus x we can find a relation between them.
In the view field of the applet you can see a mass hanging on a piece of string. This string is attached to a coil spring (which is not visible in the view field )and suspended from a ceiling. To collect "experimental" data start with defaults values and changing masses with the step of 0.05 kg , up to the total mass of 0.40 kg , record applied masses and resultant elongations. Next, calculate applied forces and graph force versus elongation rediscovering Hooke's law for a spring. According to this law elongations are proportional to applied forces, so we can write
Fe = k x
where k stands for a spring constant. This constant in your graph is its slope. Calculating this slope you will find the spring constant. Notice that you can change springs in the applet selecting the relative spring constant. Bigger the spring constant is, less elongation will result from application of the same force.
Armed with Hooke's law for a spring we are able to make some theoretical predictions about the motion of a mass attached to a coil spring. For sake of simplicity let us assume that the spring has a negligible mass and rests on a frictionless horizontal surface. Moreover, one end of the spring is attached to a fixed pole and another end is attached to an object with mass m . If the mass is pulled, the spring will be stretched (elongated) and arising force Fe will try to bring the object back to its starting position. Initially the released object will be gaining speed and kinetic energy. Reaching the starting position the object will pass it and start to compress the spring. In this process the object will be losing its speed and kinetic energy till it stops and the spring pushes it back. This qualitative discussion suggests an oscillatory motion of the object. To develop a quantitative approach, suppose that the relation Fe = k x is also valid when the spring is compressed. This means, it is valid for both positive (elongation) and negative (compression) values of x . Then Newton second law for the object can be written as follows
m Dv/Dt = - kx .
The negative sign on the right side reflects the fact that the object is always pulled or pushed by the spring toward the point with x = 0 , which is an equilibrium point. This means if the object is at x = 0 with no kinetic energy, it will stay there. Multiplying the relation above by v , rearranging it, and using the definition of v (v = Dx/Dt) we obtain
m v Dv/Dt + k x Dx/Dt = 0 .
But we already have found out that v Dv/Dt can be replaced by D(v2/2) , then x Dx/Dt due to a mathematical similarity can be replaced by D(x2/2) . This leads to
D(mv2/2)/Dt + D(kx2/2)/Dt = D(mv2/2 + kx2/2)/Dt = 0
which means that a rate of change of mv2/2 + kx2/2 must be zero, and this expression stays constant. We know that the first term of this expression represents the kinetic energy of the object. Thus, the second term must represent a potential energy related to the spring. After all it depends on the spring constant k and it is related to the elastic force Fe . This kind of energy is called an elastic potential energy.
What will change, if the system spring - mass is suspended from a ceiling? In this case beside elastic potential energy, gravitational potential energy will appear. Assuming x-axis directed vertically up, Newton second law will take a form
m Dv/Dt = - kx - mg.
The same kind of calculations as we have applied above, this time will give the following result
D(mv2/2 + kx2/2 + mgx)/Dt = 0 .
which tells us again that the total mechanical energy of the system is conserved. This time, however, beside kinetic energy and elastic potential energy we also deal with gravitational potential energy represented by the term mgx .
An explicit experimental verification of these two mechanical energy conservation laws is not quite simple because we do not know how velocity of the object depends on time and we should measure it. To do this, we should be able to measure very short times and very small distances, which without more sophisticated experimental methods is not possible. If we could apply more advanced mathematics, we would be able to recognize that Newton second law mDv/Dt = - kx - mg is the differential equation for x as a function of t , and solve this equation finding how exactly x depends on t . Therefore lack of more advanced technology and more sophisticated mathematics delays our progress. But we still are able to find "experimentally" how x depends on t and later on make an educated guess about an exact dependence. For this purpose set in the applet panel gravitation off (damping will be set automatically to none), select the mass 0.10 kg, oscillation amplitude 4.0, and number of periods 2. Start the applet and using a stopwatch collect a set of data x vs. t . The easiest way to collect such data is reading time when the bottom of the moving mass passes a meter mark. Copy the following table from the screen and record there your results. Doing it remember that deriving all formulae here we have chosen x axis positive direction up. But in the applet this choice is opposite. Therefore the x coordinates in the table below have opposite signs to these in the applet.
| x (m) | up | down | up | down |
-4 |
0 s |
-- |
||
-3 |
||||
-2 |
||||
-1 |
||||
0 |
||||
1 |
||||
2 |
||||
3 |
||||
4 |
-- |
-- |
Using the
collected data, graph carefully on a graph paper x vs.
t . Sketch on another piece of paper
the function -4cos![]() for
for ![]() from 0 to 4
from 0 to 4![]() . Comparing both graphs you should be able
to see that a dependence of x on t
may have the following form
. Comparing both graphs you should be able
to see that a dependence of x on t
may have the following form
x(t) = xo
cos(![]() t)
t)
where xo
and ![]() are certain constants. The physical
meanings of these constants is almost
obvious. For t = 0 x(0) = xo
, then xo
is the initial position which in our
particular case is - 4 m. If we take such
t = T that
are certain constants. The physical
meanings of these constants is almost
obvious. For t = 0 x(0) = xo
, then xo
is the initial position which in our
particular case is - 4 m. If we take such
t = T that ![]() T = 2
T = 2![]() then one period of the cosine
function is covered, so T is a period
of one full oscillation. Because
then one period of the cosine
function is covered, so T is a period
of one full oscillation. Because ![]() = 2
= 2![]() /T and 1/T
is called a frequency, then
/T and 1/T
is called a frequency, then ![]() is called an angular
frequency. The ordinary frequency tells how many times per
second a certain periodical phenomenon repeats itself.
is called an angular
frequency. The ordinary frequency tells how many times per
second a certain periodical phenomenon repeats itself.
If indeed x(t) has the above postulated form, how a related velocity v(t) looks like? To fond it out we have to use a relatively sophisticated mathematical method. From the definition of v(t) and the postulated form of x(t) follows
v(t) = Dx/Dt = xo[cos(![]() t) - cos(
t) - cos(![]() t -
t - ![]() Dt)]/Dt =
Dt)]/Dt =
xo[cos(![]() t) - cos(
t) - cos(![]() t)cos(
t)cos(![]() Dt) + sin(
Dt) + sin(![]() t)sin(
t)sin(![]() Dt)]/Dt
=
Dt)]/Dt
=
xo
cos(![]() t) {[1- cos(
t) {[1- cos(![]() Dt)]/Dt }+xo
sin(
Dt)]/Dt }+xo
sin(![]() t) {sin(
t) {sin(![]() Dt)/Dt }.
Dt)/Dt }.
Now we have to find out values of
both figured brackets for Dt = 0. Straight
forward insertion of 0 instead Dt gives
in both cases the same result 0/0 which might
be any number. Let us simplify the first figure bracket using
well known trigonometric identity cos![]() = cos2(
= cos2(![]() /2) - sin2(
/2) - sin2(![]() /2). The
result of it after some additional algebraic
manipulations is
/2). The
result of it after some additional algebraic
manipulations is
v(t) = xo
cos(![]() t)
t) ![]() 2(Dt/2){sin(
2(Dt/2){sin(![]() Dt/2)/(
Dt/2)/(![]() Dt/2) }2
+ xo
Dt/2) }2
+ xo ![]() sin(
sin(![]() t) {sin(
t) {sin(![]() Dt)/(
Dt)/(![]() Dt) }.
Dt) }.
These manipulations were used to
present the contents of both figured brackets in the form of sin(![]() )/
)/![]() , where instead of
, where instead of ![]() in the first bracket
there is
in the first bracket
there is ![]() Dt/2
and in the second bracket there is
Dt/2
and in the second bracket there is ![]() Dt. As
Dt. As ![]() approaches zero this ratio
approaches 1. A kind of intuitive justification (not a strict
mathematical proof) of this can be presented as follows. The
angle
approaches zero this ratio
approaches 1. A kind of intuitive justification (not a strict
mathematical proof) of this can be presented as follows. The
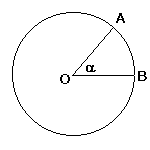
angle ![]() in radians
(see Fig.1) is equal to arch(AB)/OA, whereas sin(
in radians
(see Fig.1) is equal to arch(AB)/OA, whereas sin(![]() ) (see Fig.2) is
equal to AC/OA. Then sin(
) (see Fig.2) is
equal to AC/OA. Then sin(![]() )/
)/![]() = AC/arch(AB). But looking at Fig.
2 we can see that as
= AC/arch(AB). But looking at Fig.
2 we can see that as ![]() approaches zero the difference between AC
and arch(AB) is getting smaller.
approaches zero the difference between AC
and arch(AB) is getting smaller.
 |
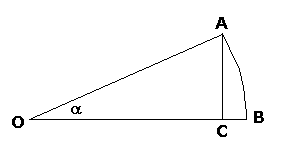 |
Fig. 1 |
Fig. 2 |
Applying the last result to the expression for v(t) we end up with the simple result
v(t) = xo
![]() sin(
sin(![]() t) .
t) .
The same method applied to Dv(t)/Dt results with the acceleration
a(t) = - xo
![]() 2
cos(
2
cos(![]() t) .
t) .
Inserting the results for x(t) and a(t) into the Newton second law for the spring (harmonic oscillator) we obtain the following result
![]() = [k/m]�
or T
= 2
= [k/m]�
or T
= 2![]() [m/k]�
.
[m/k]�
.
You can easily verify this last result "experimentally" because you already have found k (for its relative value equal to 1) and you have the graph of "experimental" x(t) made for m = 0.10 kg. Inserting the values for k and m to the formula for T you can find the time of a single full oscillation. You also can find "experimental" value of T from the graph of x(t). If these two values of T are almost identical the theoretical predictions including the mechanical energy conservation principle are confirmed.
Evaluation
If at this point you can solve the
following problems:
If a harmonic oscillator is transferred from our strange planet with g = 0.01 m/s2 to the Earth, will its period be changed?
If an object is thrown up is its potential energy changing? Is its kinetic energy changing? Is its mechanical energy changing if air resistance can be neglected?
If a harmonic oscillator of mass m and spring constant k has initial velocity vo and initial position xo what is its mechanical energy at any moment of time?
Using the same methods as
for v(t), show that for a harmonic
oscillator (spring) a(t) = - xo
![]() 2
cos(
2
cos(![]() t).
t).
If we consider a real harmonic oscillator made with a coil spring of considerable mass, will the mass of the spring influence the frequency of this oscillator?
Can kinetic energy of an object be transformed into potential energy (or vice versa) if there is no force acting on this object? If so, think about an example.
Two alike electric charges repeal each other. Can you store potential energy in such system?
the objectives of this lesson are fully achieved. If you have doubts try to read it once more concentrating on them, but do not try to memorize this text. Physics is not about memorizing, it is about understanding.
Since February 1997 you are visitor
| Last update: Jan 10, 1997 | E - mail to Edward Kluk |
| Copyright (c) 1996 Edward Kluk | |