Pursuit-EvasionPursuit-evasion problems have a long history, dating back at least to the 1700's, when Bouguer considered the problem of pirates chasing merchant ships on the high seas. In the twentieth century, game theory emerged as the mathematical tool most often used to formalize and solve these problems. In the 21st century, my own work in this area began, when Rafael Murrieta arrived for a three-year stay at my lab in the Beckman Institute. Our collaboration began with what we expected to be a simple question: Is it possible for a pursuer to maintain visibility of an evader in an environment containing polygonal obstacles. Some years down the road, we still don't know the complete answer to this question --- but we have made some progress. And along the way, we have studied a few related pursuit-evasion problems. Pursuit-evasion problems come in many varieties. Perhaps the most famous problems involve a pursuer and an evader, both with finite speed, moving in an obstacle-free environment (the homicidal chauffeur is such a problem). Search problems, in which the pursuer is tasked with finding the evader, are also considered to be pursuit-evasion problems. Problems in which pursuers serve as guards to protect a target from invasion (in this case, the invaders attempt to reach the target while evading the guards) can also be considered as pursuit-evasion problems. My group has worked on each of these problems (and their variations), and some of that work is summarized below. Surveillance Problems Search Barrier Coverage | |
| | |
Sufficient Conditions for EscapeMurrieta, Muppirala, Sarmiento, Bhattacharya, and Seth Hutchinson | |
 |
This work addresses the pursuit-evasion problem of maintaining surveillance by
a pursuer of an evader in a world populated by polygonal obstacles. This
requires the pursuer to plan collision-free motions that honor distance
constraints imposed by sensor capabilities, while avoiding occlusion of the
evader by any obstacle.
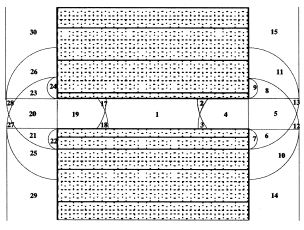
Our method extends the three-dimensional cellular
decomposition of Schwartz and Sharir to represent the four-dimensional
configuration space of the pursuer-evader system, and derive necessary
conditions for surveillance (equivalently, sufficient conditions for escape) in
terms of this new representation. A game theoretic formulation of the problem is
then given, and this formulation is used to characterize optimal escape
trajectories for the evader.
A shooting algorithm is proposed that finds these
trajectories using the minimum principle. Finally, noting the similarities
between this surveillance problem and the problem of cooperative manipulation
by two robots, several cooperation strategies are presented that maximize
system performance for cooperative motions.
The figure on the left shows the decomposition of the evader's workspace. |
| This work is described in our IJRR paper: Back to top | |
| | |
Motion Strategies for Surveillance - Complete Strategies for a Simple EnvironmentBhattacharya, Candido and Hutchinson | |
 |
This work addresses
the problem of surveillance in an environment with a single obstacle
consisting of two half-lines anchored at a vertex.
We showed that the problem of tracking an evader with one pursuer around one corner
is completely decidable.
The pursuer and evader are assumed to have complete
information about each other's instantaneous position and velocity.
We derived a partition of the visibility region of the pursuer
based on the region in which the evader lies,
and provided strategies for the evader to escape the
visibility region of the pursuer or for the pursuer to track the target for all
future time.
We also presented the solution to the inverse problem: given the
position of the evader, the positions of the pursuer for which the evader can
escape the visibility region of the target.
These results have been provided
for varying speeds of the pursuer and the evader.
Based on the results of the inverse problem we provided
an algorithm that can decide if the evader can escape from
the visibility region of a pursuer for some initial
pursuer and evader positions.
Finally, we extended the result of the target
tracking problem around a corner in two dimensions to an edge in three dimensions.
The figure on the left shows the decomposition of the workspace for a given pursuer initial configuration. |
| This work is described in our RSS paper: Back to top | |
| | |
Approximation Schemes for Two-Player Pursuit Evasion Games with Visibility ConstraintsBhattacharya and Hutchinson | |
 |
In this work, we consider the problem in which a mobile pursuer attempts to
maintain visual contact with an evader as it moves through an environment
containing obstacles. This surveillance problem is a variation of traditional
pursuit-evasion games, with the additional condition that the pursuer
immediately loses the game if at any time it loses sight of the evader.
Since it has been shown that the problem of deciding whether or not the pursuer is
able to maintain visibility of the evader is at least NP-complete, we present
schemes to approximate the set of initial positions of the pursuer from which
it might be able to track the evader. We first consider the case of an
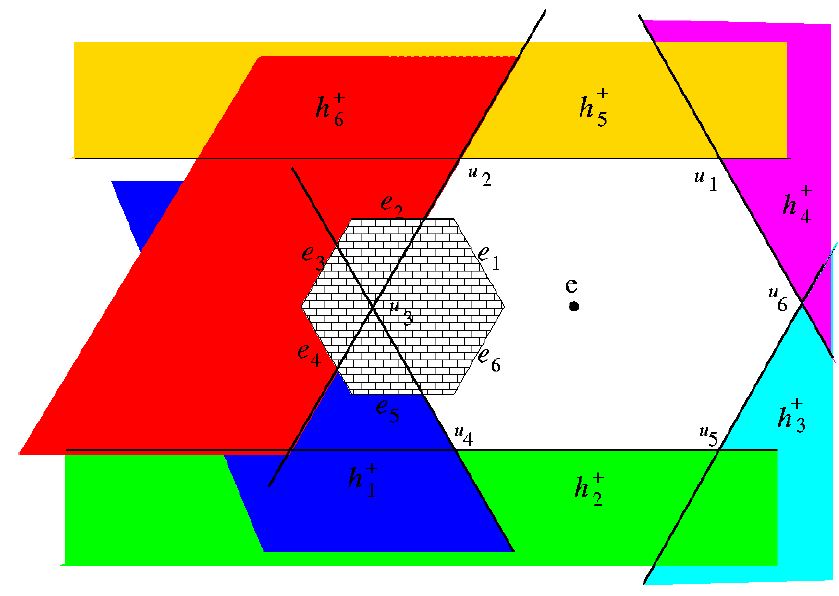
environment containing only polygonal obstacles. We prove that in this case the
set of initial pursuer configurations from which it does not lose the game is
bounded. Moreover, we provide polynomial time approximation schemes to bound
this set. We then extend our results to the case of arbitrary obstacles with
smooth boundaries.
The figure on the left shows the set of regions from which the pursuer cannot track the evader (in various colors) for an environment containing a single hexagonal obstacle. The white polygon containing the evader defines the set of points from which the pursuer may be able to successfully track the evader. |
| This work is described in our RSS paper: Back to top | |
| | |
Nash Equilibrium Strategies for a Two-player Pursuit.Evasion Game with Visibility ConstraintsS. Bhattacharya and Seth Hutchinson | |
 |
In this work, we give a game-theoretic analysis of a visibility-based
pursuit-evasion game in a planar environment containing obstacles.
The pursuer
and the evader are holonomic having bounded speeds.
Both players have a complete map of the environment.
Both players have omnidirectional vision and
have knowledge about each other's current position as long as they are visible
to each other.
The pursuer wants to maintain visibility of the evader for the
maximum possible time and the evader wants to escape the pursuer's sight as
soon as possible.
Under this information structure, we present necessary and
sufficient conditions for surveillance and escape.
We present strategies for the players that are in Nash equilibrium.
The strategies are a function of the
value of the game.
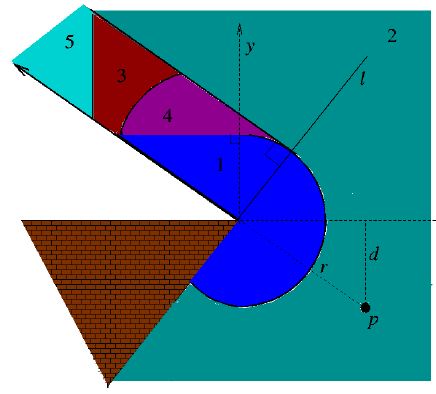
Using these strategies, we construct a value function by
integrating the adjoint equations backward in time from the termination
situations provided by the corners in the environment.
From these value functions we recompute the control strategies for the
players to obtain optimal trajectories for the players
near the termination situation.
This is the first work that presents the necessary and sufficient conditions
for tracking for a visibility based pursuit-evasion game
and presents the equilibrium strategies for the players.
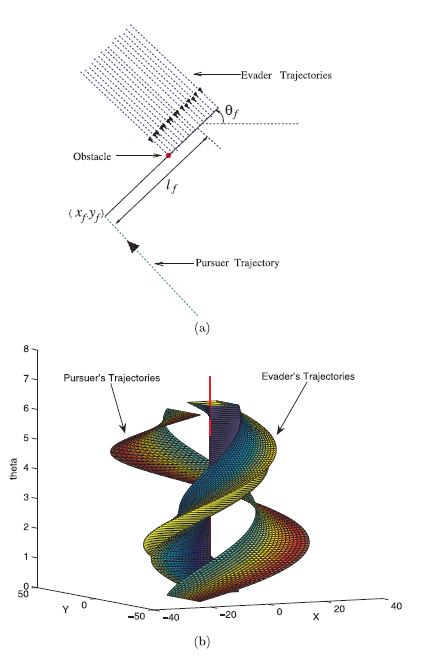
The figure to the left shows the optimal trajectories for an environment having a single point obstacle: (a) optimal trajectories in the plane; (b) optimal trajectories across a section in R^3 x S^1. |
| This work is described in our IJRR paper: Back to top | |
| | |
Expected-Time Optimal SearchSarmiento, Murrieta and Seth Hutchinson | |
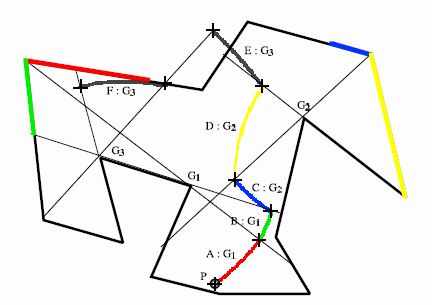 |
In this work we address the problem of finding time-optimal search paths in
known environments, in particular, the problem of searching a known
environment for an object whose unknown location is characterized by a known
probability density function (pdf).
With this formulation, the time required to
find the object is a random variable induced by the choice of search path
together with the pdf for the object's location. The optimization problem we
consider is that of finding the path that minimizes the expected value of the
time required to find the object. As the complexity of the problem precludes
finding an exact optimal solution, we propose a two-level, heuristic approach
to finding the optimal search path. At the top level, we use a decomposition of
the workspace based on critical curves to impose a qualitative structure on the
solution trajectory. At the lower level, individual segments of this trajectory
are refined using local numerical optimization methods. We have implemented the
algorithm and presented simulation results for the particular case when the
object's location is specified by the uniform pdf.
The figure to the left shows the locally optimal trajectory to search the polygon starting from point P. |
| This work is described in our Advanced Robotics paper: Back to top | |
| | |
Barrier CoverageKloder and Seth Hutchinson | |
|
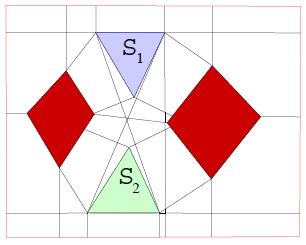
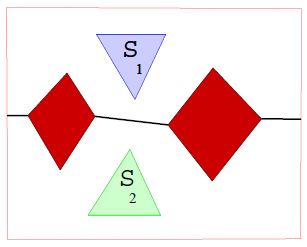
Barrier coverage is problem of preventing undetected intrusion in
a particular region using robot sensors.
We have investigated this problem for the case in which the available
sensors are sufficient to construct a barrier (complete barrier
coverage), and for the case in which there are not enough
sensors to construct a full barrier (partial barrier coverage).
For the case of complete barrier coverage, we solve the problem of finding the minimum-length barrier using variable bounded-range line-of-sight sensors in a two-dimensional polygonally-bounded region. To do this, we build a graph of candidate barriers (the Barrier Candidate Graph) that could potentially be in the minimum barrier. The dual of this graph shows the connectivity of the free space. We thus reduce the problem to the network flows maximum-flow/minimum-cut problem. For the problem of partial barrier coverage, we frame the problem as that of using robot sensors (guards) to minimize the probability of undetected intrusion in a particular region by an intruder. We use ideas from noncooperative game theory together with previous results from complete barrier coverage - the problem of completely preventing undetected intrusion - to develop new methods that solve this problem for the specific case of bounded-range line-of-sight sensors in a two-dimensional polygonally-bounded region. Our solution constructs equilibrium strategies for the intruder and guards, and calculates the level of partial coverage. The figure to the left shows the barrier candidate graph and the minimal complete barrier for a polygonal environment. |
This work is described in Stephen's two ICRA papers:
| |
| | |
 |
Seth Hutchinson |
Roboticist |